Kapitel 8 Schätzen von Verteilungsparametern
Mit diesem Kapitel beginnt die schließende oder induktive Statistik, mit der wir anhand von Stichproben etwas über größere Grundgesamtheiten aussagen möchten. Der Anspruch geht also über die beschreibende oder deskriptive Statistik hinaus, wobei die Wahrscheinlichkeitstheorie und Verteilungen (Kapitel 6 und 7) gewissermaßen die Brücke zwischen den beiden Teilbereichen der Statistik bilden, um bei dem Bild von Zimmermann-Janschitz (2014) zu bleiben.
Die deskriptive Statistik wird uns die nächsten sechs Wochen beschäftigen. Nach diesem Kapitel zu Schätzen von Verteilungsparametern gibt es ein Kapitel zu statistischen Tests (Kapitel 9), das wir über drei Wochen lesen werden, und abschließend Kapitel 10 zu linearer Regression, das wir über zwei Wochen lesen werden. In Kapitel 10 werden viele Lehrveranstaltungsinhalte zusammen kommen - also bleiben Sie dran.
In diesem Kapitel diskutieren wir:
- die Anforderungen an Schätzer
- den Schätzer des Mittelwertes \(\mu\) einer Normalverteilung und dessen Standardfehler und Konfidenzintervall
- den Schätzer der Standardabweichung \(\sigma\) einer Normalverteilung
- das Quantil-Quantil-Diagramm (QQ-Plot) als visueller Verteilungstest
Zunächst aber ein paar Worte zum Grundprinzip der schließenden Statistik (vgl. Mittag (2016), Abb. 14.1, S. 212). Wie wir wissen ist eine Stichprobe (im besten Fall) eine zufällige Auswahl von Merkmalsträgern aus einer Grundgesamtheit von Merkmalsträgern. In der schließenden Statistik geht es jetzt um die Verdichtung der Informationen in der Stichprobe in Form von Stichprobenfunktionen, mit denen wir bestimmte Parameter der Grundgesamtheit schätzen. Im Fall von Verteilungsparametern handelt es sich bei den Stichprobenfunktionen v.a. um den Mittelwert und die Standardabweichung.
8.1 Anforderungen an Schätzer
Die Parameter der Stichprobe (Mittelwert, Standardabweichung etc.) dienen als Schätzer der Parameter der Grundgesamtheit. Die Anforderungen an einen solchen Schätzer sind:
- Erwartungstreue: Der Schätzer soll den wahren (unbekannten) Wert der Grundgesamtheit möglichst genau wiedergeben
- Konsistenz: Die Genauigkeit der Schätzung soll mit wachsender Stichprobengröße zunehmen
- Effizienz: Unterschiede der Schätzwerte sollen bei Ziehung verschiedener Stichproben möglichst gering sein
In wie weit diese Anforderungen erfüllt sind ergibt sich aus dem statistischen Modell der Grundgesamtheit, z.B. dass Merkmalsausprägungen normalverteilt ist. Schauen Sie sich dazu nochmal Kapitel 7 an. Die Abbildungen 7.2 und 7.3 zeigen wie wir von der empirischen zur theoretischen Verteilung kommen. In Abbildungen 7.5 und 7.6 sehen wir die Normalverteilung als ein solches theoretisches Modell der Grundgesamtheit für verschiedene Konstellationen der Parameter \(\mu\) und \(\sigma\).
Da die Stichprobendaten als Realisationen von Zufallsvariablen interpretiert werden (vgl. Kapitel 7), ist auch der aus ihnen errechnete Schätzwert eine Realisation einer Zufallsvariable, die Schätzer genannt wird. Dazu die folgende Notation:
- für einen nicht näher spezifizierten Parameter verwenden wir das Symbol \(\theta\) (“theta”)
- den Schätzer dieses Parameters bezeichnen wir mit \(\hat\theta\) (“theta-Dach”)
- ein Parametervektor wird fett gedruckt: \(\boldsymbol\theta=\begin{pmatrix}\theta_1 & \theta_2 & \cdots & \theta_p\end{pmatrix}\)
- z.B. Im Fall der Normalverteilung: \(X\sim N(\boldsymbol\theta=\begin{pmatrix}\mu & \sigma\end{pmatrix}\))
Erwartungstreue bedeutet mathematisch: \[\begin{equation} E(\hat\theta)=\theta \tag{8.1} \end{equation}\]
In Worten: Der Erwartungswert des Schätzers ist der wahre Wert des Parameters. D.h. der Schätzer trifft “im Mittel” (bei wiederholter Stichprobenziehung) den zu schätzenden Wert genau.
Wenn ein Schätzer nicht erwartungstreu ist, heißt die Differenz Verzerrung oder Bias: \[\begin{equation} B(\hat\theta)=E(\hat\theta)-\theta \tag{8.2} \end{equation}\]
Ein verzerrter Schätzer, dessen Verzerrung gegen Null geht wenn der Stichprobenumfang \(n\) gegen Unendlich geht heißt asymptotisch erwartungstreu: \[\begin{equation} \lim_{n\to\infty}E(\hat\theta)=\theta \tag{8.3} \end{equation}\]
8.2 Normalverteilung: Schätzer für \(\mu\)
Der Schätzer für \(\mu\) ist: \[\begin{equation} \hat\mu=\bar x \tag{8.4} \end{equation}\]
In Worten: Der Schätzer des Mittelwertes einer normalverteilten Grundgesamheit \(\hat\mu\) ist der arithmetische Mittelwert einer Stichprobe aus dieser Grundgesamtheit.
Der Schätzer wird in der Regel nicht exakt mit dem wahren Wert übereinstimmen, nur im Mittel (bei wiederholter Stichprobenziehung) - er ist erwartungstreu (s.o.). Da \(\hat\mu\) als Zufallsvariable interpretiert wird, kann diese Unsicherheit als sogenannter Standardfehler des Mittelwertschätzers \(s_{\hat\mu}\) ausgedrückt werden: \[\begin{equation} s_{\hat\mu}=\frac{s}{\sqrt{n}} \tag{8.5} \end{equation}\]
Wobei \(s\) die Standardabweichung der Stichprobe ist (vgl. Kapitel 4) und \(n\) der Stichprobenumfang. Wir sehen an der Formel, dass je kleiner die Standardabweichung der Stichprobe ist und je größer der Stichprobenumfang ist desto besser die Schätzung wird - das ist die o.g. Konsistenzeigenschaft, die wir von einem Schätzer erwarten.
Der Standardfehler wird mit wahrscheinlichkeitstheoretischen Annahmen verknüpft und geht so in die Berechnung des sogenannten Konfidenzintervalls ein, das die Unsicherheit des Schätzers mit Wahrscheinlichkeiten ausdrückt. Das Konfidenzintervall des Mittelwertschätzers wollen wir im Folgenden einmal herleiten. Das bildet die Grundlage für viele ähnliche Herleitungen, die später bei den Tests und bei der Regression kommen, die wir dann aber nicht mehr so ausführlich behandeln werden.
Unter Annahme einer normalverteilten Grundgesamtheit folgt der standardisierte Schätzer des Mittelwertes bei wiederholtem Stichprobenziehen einer sogenannten t-Verteilung: \[\begin{equation} \frac{\hat\mu-\mu}{s_{\hat\mu}}\sim t_{n-1} \tag{8.6} \end{equation}\]
Die Herleitung können Sie z.B. in Mittag (2016), S. 218ff nachlesen. Hier soll uns nur die Bedeutung dieser Formel interessieren. \(\hat\mu-\mu\) ist die Differenz des Schätzers vom wahren Mittelwert (den wir nicht kennen). Diese Differenz wird mit dem Standardfehler des Schätzers \(s_{\hat\mu}\) standardisiert. Das Symbol \(\sim\) (“Tilde”) heißt “ist verteilt gemäß” (vgl. Kapitel 7). Und \(t_{n-1}\) steht für die t-Verteilung, die einen Parameter hat (genannt “Freiheitsgrade”), der hier den Wert \(n-1\) annimmt. Man spricht von einer t-Verteilung mit \(n-1\) Freiheitsgraden. Je größer diese Zahl desto schmaler die t-Verteilung. Abbildung 8.1 zeigt die t-Verteilung für verschiedene Freiheitsgrade. Wenn \(n\) gegen Unendlich geht, dann geht die t-Verteilung in die Standardnormalverteilung \(N(0,1)\) über (vgl. Abbildung 7.4). Man sieht in Abbildung 8.1, dass sich schon zwischen 100 und 1000 Freiheitsgraden nicht mehr viel an der Breite der t-Verteilung ändert. Wie die Standardnormalverteilung geht die t-Verteilung von \(-\infty\) bis \(+\infty\) und ist symmetrisch um einen Mittelwert 0. D.h. mit dieser Verteilung erwarten wir bei wiederholter Stichprobenziehung im Mittel den wahren Mittelwert der Grundgesamtheit genau zu schätzen, \(E\left(\hat\mu-\mu\right)=0\). Aber von Stichprobe zu Stichprobe erwarten wir eine Variation des Schätzwertes gemäß der t-Verteilung, Formel (8.6).
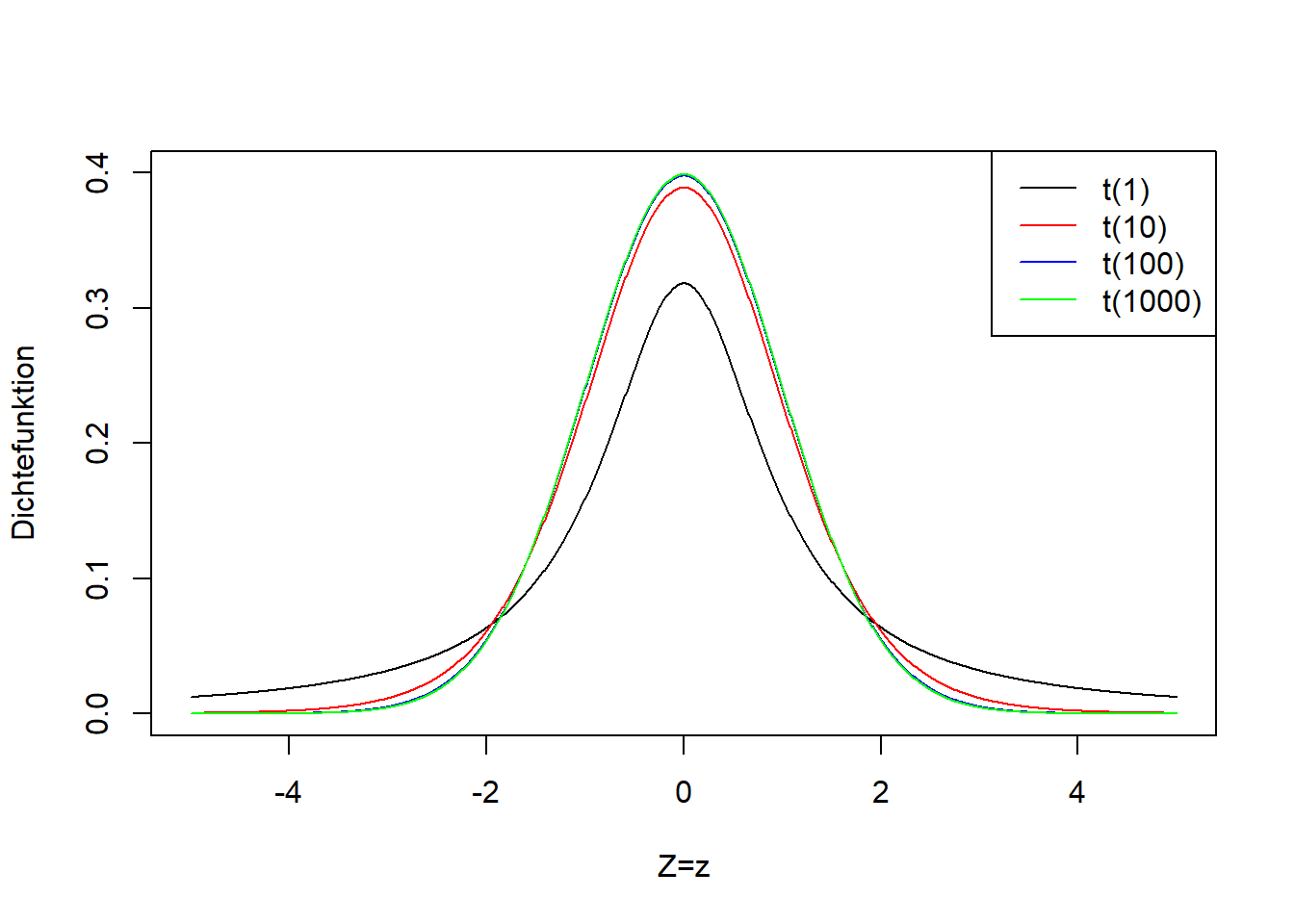
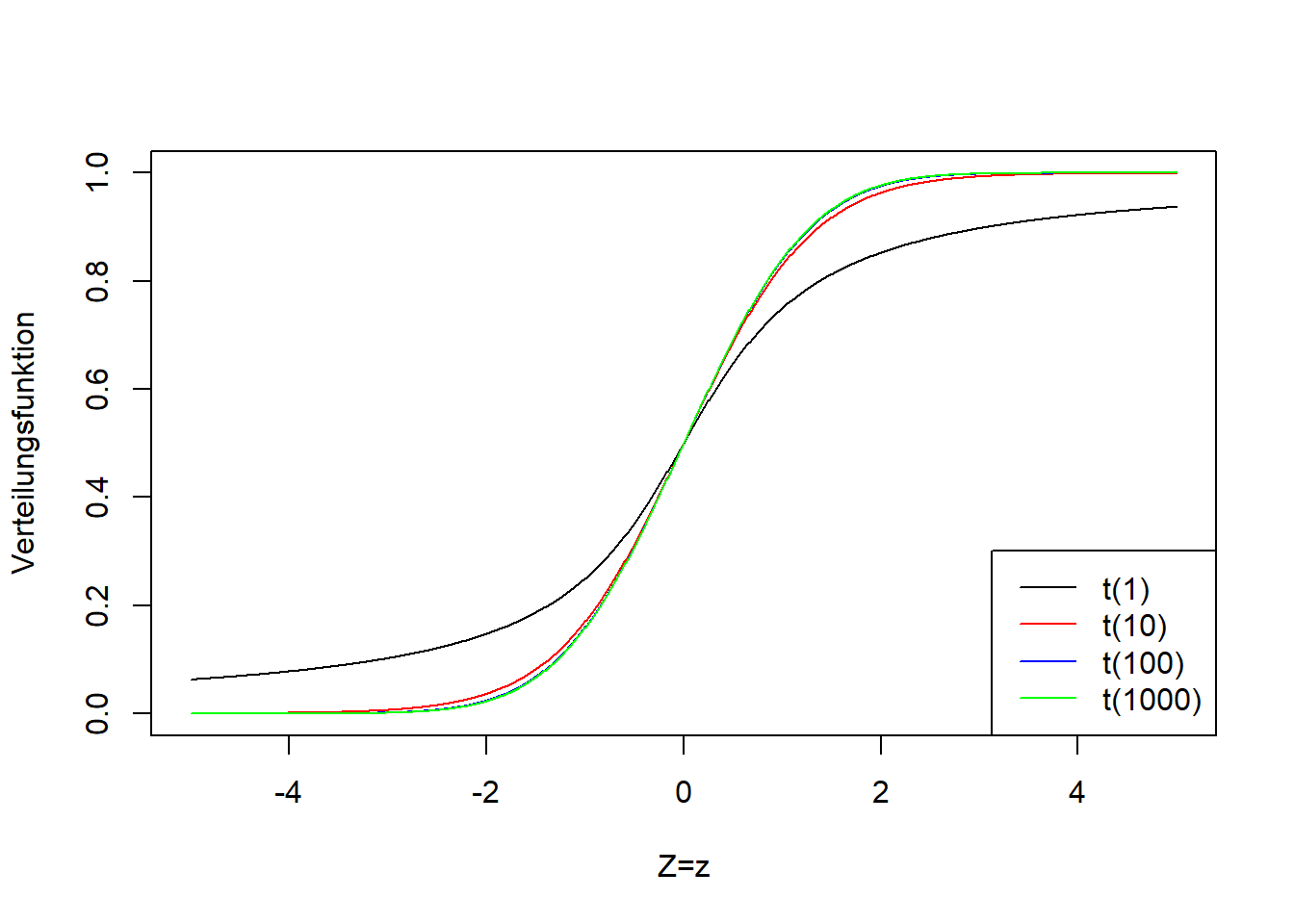
Abbildung 8.1: Links: Dichtefunktion der t-Verteilung einer beliebigen Zufallsvariable \(Z\) für verschiedene Freiheitsgrade (der einzige Parameter der t-Verteilung heißt “Freiheitsgrade”). Rechts: Verteilungsfunktion der entsprechenden t-Verteilungsvarianten.
Das zentrale 95% Konfidenzintervall einer beliebigen Zufallsvariablen \(Z\sim t_{n-1}\) ist: \[\begin{equation} \Pr\left(-t_{n-1;0.975}\leq Z\leq t_{n-1;0.975}\right)=0.95 \tag{8.7} \end{equation}\]
\(t_{n-1;0.975}\) steht für das 0.975-Quantil der t-Verteilung mit \(n-1\) Freiheitsgraden (Abbildung 8.2). Da die t-Verteilung symmetrisch ist gilt \(-t_{n-1;0.975}=t_{n-1;0.025}\).
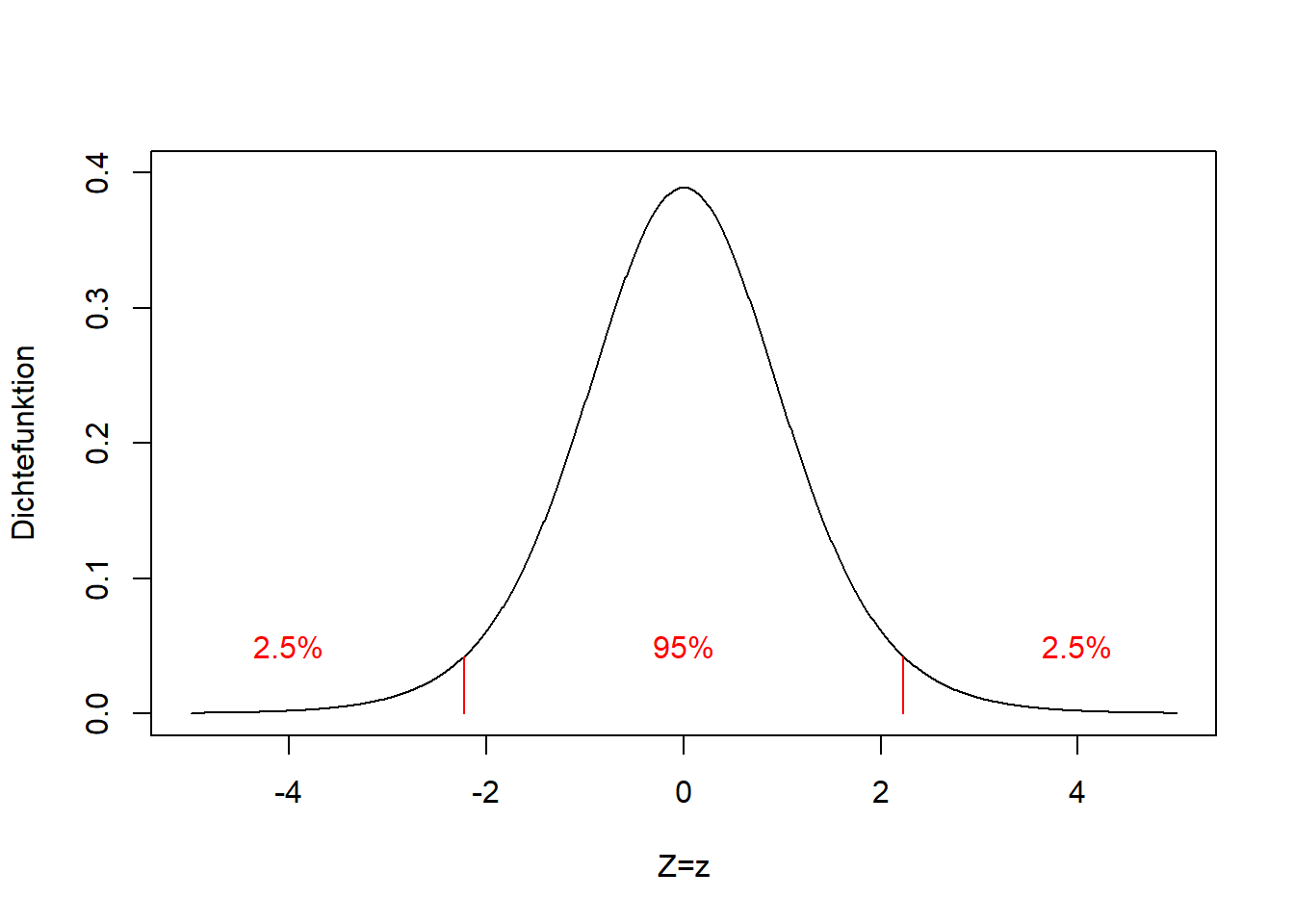
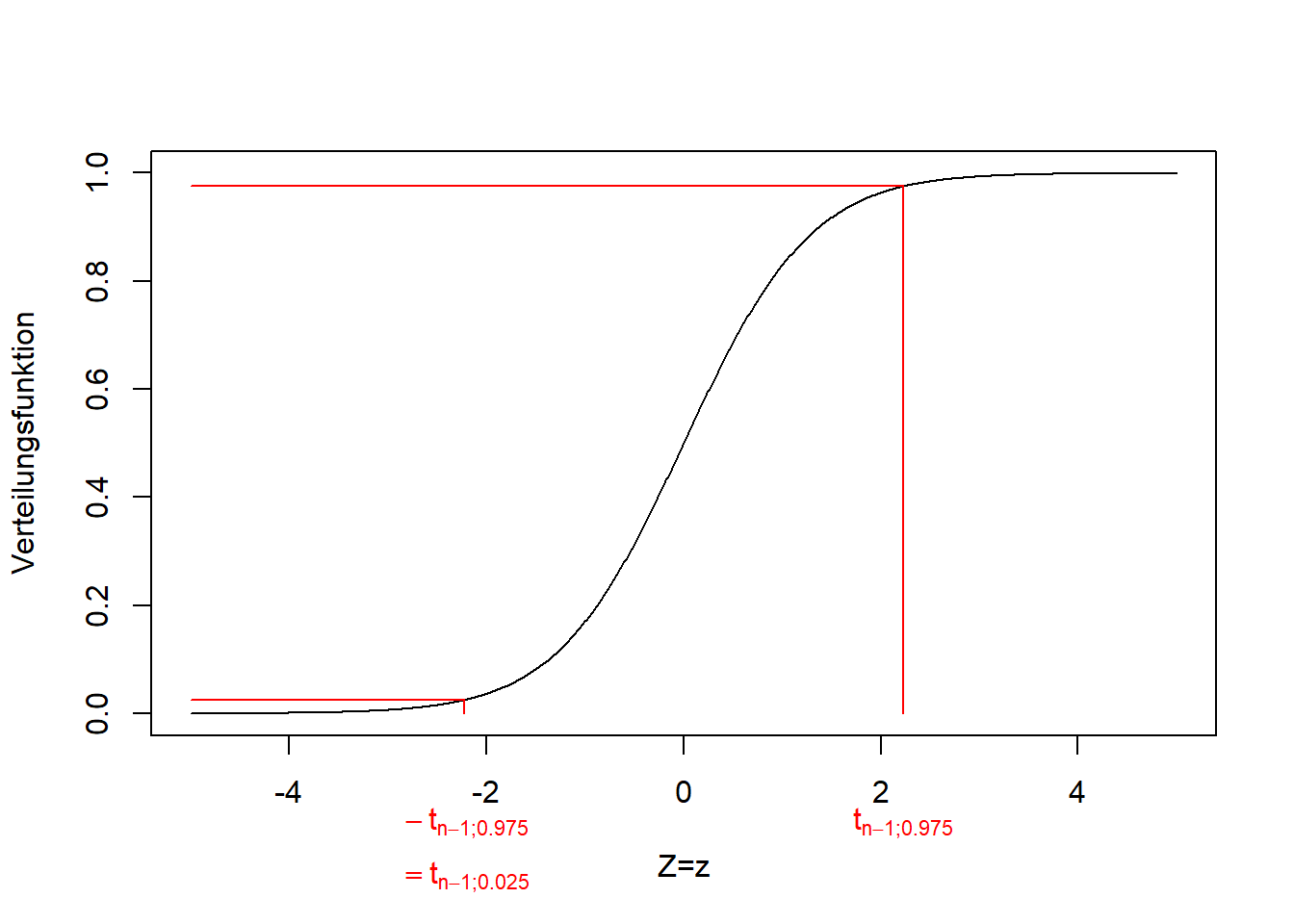
Abbildung 8.2: Links: Dichtefunktion der t-Verteilung einer beliebigen Zufallsvariable \(Z\), hier mit 10 Freiheitsgraden. Die Grenzen des zentralen 95% Konfidenzintervalls sind rot markiert. Es umschließt die zentralen 95% der Verteilung, so dass 2.5% links und 2.5% rechts davon liegen. Rechts: Verteilungsfunktion der entsprechenden t-Verteilung. Die Grenzen des Konfidenzintervalls kann man hier direkt ablesen, als 0.025- und 0.975-Quantile. Da die t-Verteilung symmetrisch ist gilt \(-t_{n-1;0.975}=t_{n-1;0.025}\).
Setzen wir nun Formel (8.6) für \(Z\) in Formel (8.7) ein erhalten wir: \[\begin{equation} \Pr\left(-t_{n-1;0.975}\leq\frac{\hat\mu-\mu}{s_{\hat\mu}}\leq t_{n-1;0.975}\right)=0.95 \tag{8.8} \end{equation}\]
Multplizieren der inneren Ungleichung mit \(s_{\hat\mu}\) ergibt: \[\begin{equation} \Pr\left(-t_{n-1;0.975}\cdot s_{\hat\mu}\leq\hat\mu-\mu\leq t_{n-1;0.975}\cdot s_{\hat\mu}\right)=0.95 \tag{8.9} \end{equation}\]
Subtraktion von \(\hat\mu\) ergibt: \[\begin{equation} \Pr\left(-\hat\mu-t_{n-1;0.975}\cdot s_{\hat\mu}\leq-\mu\leq -\hat\mu+t_{n-1;0.975}\cdot s_{\hat\mu}\right)=0.95 \tag{8.9} \end{equation}\]
Und schlussendlich Multiplikation mit \(-1\): \[\begin{equation} \Pr\left(\hat\mu-t_{n-1;0.975}\cdot s_{\hat\mu}\leq\mu\leq \hat\mu+t_{n-1;0.975}\cdot s_{\hat\mu}\right)=0.95 \tag{8.10} \end{equation}\]
Merke: Um den letzten Schritt zu verstehen muss man wissen, dass sich bei der Multiplikation einer Ungleichung mit einer negativen Zahl die Vergleichszeichen (hier \(\leq\)) umdrehen. Danach wurde die Ungleichung wieder von klein nach groß geordnet.
Setzen wir nun die Formeln (8.4) und (8.5) in Formel (8.10) ein erhalten wir: \[\begin{equation} \Pr\left(\bar x-t_{n-1;0.975}\cdot\frac{s}{\sqrt{n}}\leq\mu\leq\bar x+t_{n-1;0.975}\cdot\frac{s}{\sqrt{n}}\right)=0.95 \tag{8.11} \end{equation}\]
Das ist nun das zentrale 95% Konfidenzintervall, das besagt: Die Wahrscheinlichkeit, dass der wahre Wert \(\mu\) größer oder gleich \(\bar x-t_{n-1;0.975}\cdot\frac{s}{\sqrt{n}}\) und kleiner oder gleich \(\bar x+t_{n-1;0.975}\cdot\frac{s}{\sqrt{n}}\) ist, ist 0.95. Man kann das Konfidenzintervall auch mit den Intervallgrenzen so schreiben: \[\begin{equation} KI=\left[\bar x-t_{n-1;0.975}\cdot\frac{s}{\sqrt{n}};\bar x+t_{n-1;0.975}\cdot\frac{s}{\sqrt{n}}\right] \tag{8.12} \end{equation}\]
Beachten Sie die Interpretation des Konfidenzintervalls, die sich aus dem klassischen Wahrscheinlichkeitsbegriff ergibt (vgl. Kapitel 6): Bei hypothetischer wiederholter Stichprobenziehung des selben Umfangs aus der selben Grundgesamtheit enthält in 95% der Fälle das Konfidenzintervall den wahren Wert, während die restlichen 5% der Intervalle den wahren Wert nicht enthalten (Abbildung 8.3). Für die einzige Stichprobe, die wir jeweils vorliegen haben ist das keine Wahrscheinlichkeit, dass der wahre Wert in den Grenzen des Konfidenzinervalls liegt! Das wird in der Praxis often verwechselt, also behalten Sie sich das gut.
# plot 1: 5 Zufallszahlen
# initialise
xbar <- rep(NA,50)
ki <- cbind(rep(NA,50),rep(NA,50))
# Schleife über 50 Wiederholungen
for(i in 1:50){
# ziehe 5 Zufallszahlen aus Standardnormalverteilung N(0,1)
n <- 5
x <- rnorm(n, mean=0, sd=1)
# Mittelwert
xbar[i] <- mean(x)
# zentrales 95% Konfidenzintervall
ki[i,1:2] <- xbar[i] + c(-1,1)*qt(0.975,df=n-1)*sd(x)/sqrt(n)
}
# plotte Mittelwerte und Konfidenzintervalle für Wiederholungen
wh <- seq(1,50,1)
plot(wh, xbar, type='p', pch=15, ylim=c(-4,4),
xlab="Wiederholung", ylab="Mittelwertschätzer", main="n=5")
segments(x0=wh, y0=ki[,1], x1=wh, y1=ki[,2])
# markiere jene Wiederholungen rot,
# deren Konfidenzintervall nicht den wahren Mittelwert 0 einschließt
id <- ki[,1] >= 0 | ki[,2] <= 0
points(wh[id], xbar[id], pch=15, col="red")
segments(x0=wh[id], y0=ki[id,1], x1=wh[id], y1=ki[id,2], col="red")
# plot 2: 10 Zufallszahlen
# initialise
xbar <- rep(NA,50)
ki <- cbind(rep(NA,50),rep(NA,50))
# Schleife über 50 Wiederholungen
for(i in 1:50){
# ziehe 10 Zufallszahlen aus Standardnormalverteilung N(0,1)
n <- 10
x <- rnorm(n, mean=0, sd=1)
# Mittelwert
xbar[i] <- mean(x)
# zentrales 95% Konfidenzintervall
ki[i,1:2] <- xbar[i] + c(-1,1)*qt(0.975,df=n-1)*sd(x)/sqrt(n)
}
# plotte Mittelwerte und Konfidenzintervalle für Wiederholungen
wh <- seq(1,50,1)
plot(wh, xbar, type='p', pch=15, ylim=c(-4,4),
xlab="Wiederholung", ylab="Mittelwertschätzer", main="n=10")
segments(x0=wh, y0=ki[,1], x1=wh, y1=ki[,2])
# markiere jene Wiederholungen rot,
# deren Konfidenzintervall nicht den wahren Mittelwert 0 einschließt
id <- ki[,1] >= 0 | ki[,2] <= 0
points(wh[id], xbar[id], pch=15, col="red")
segments(x0=wh[id], y0=ki[id,1], x1=wh[id], y1=ki[id,2], col="red")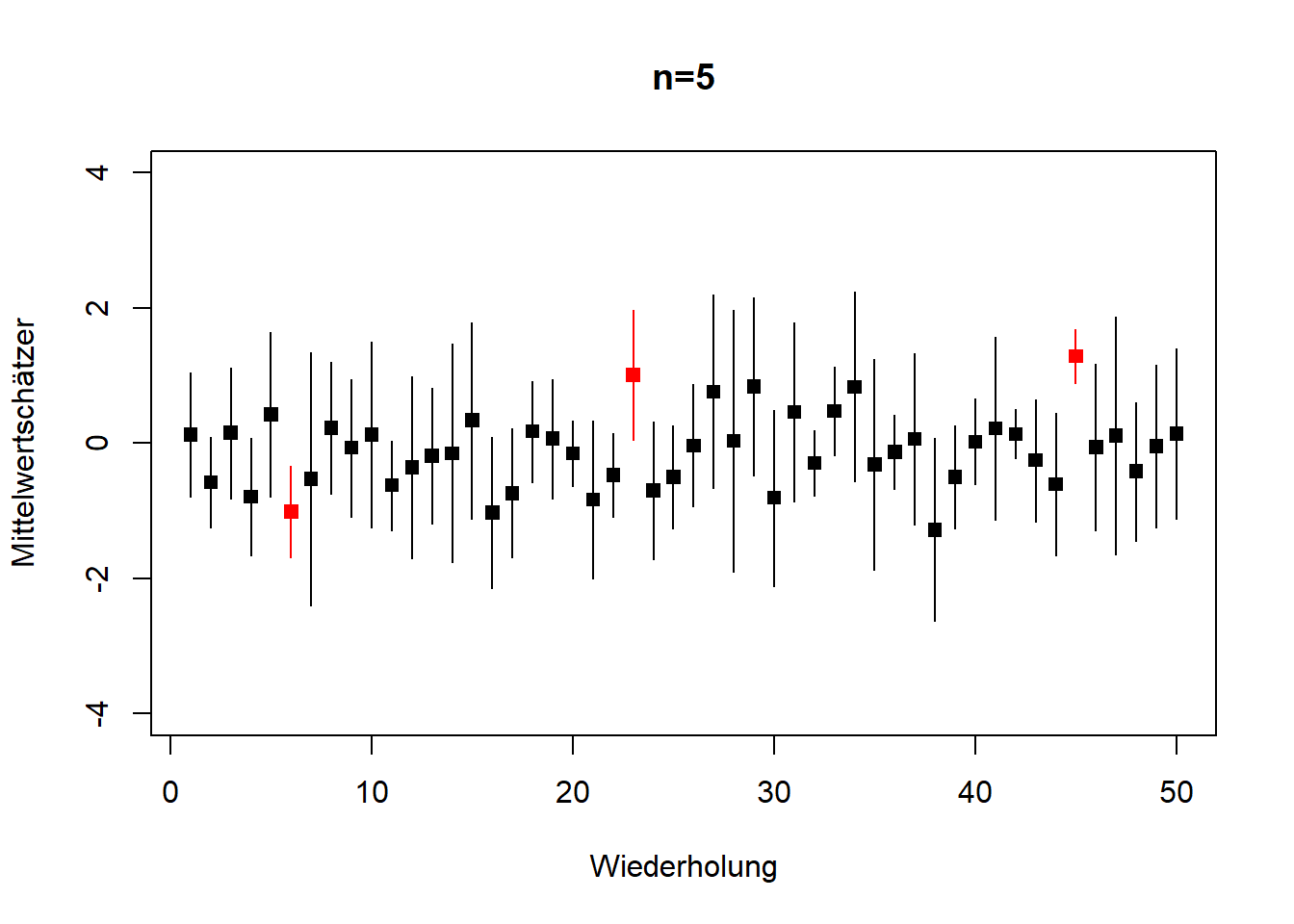
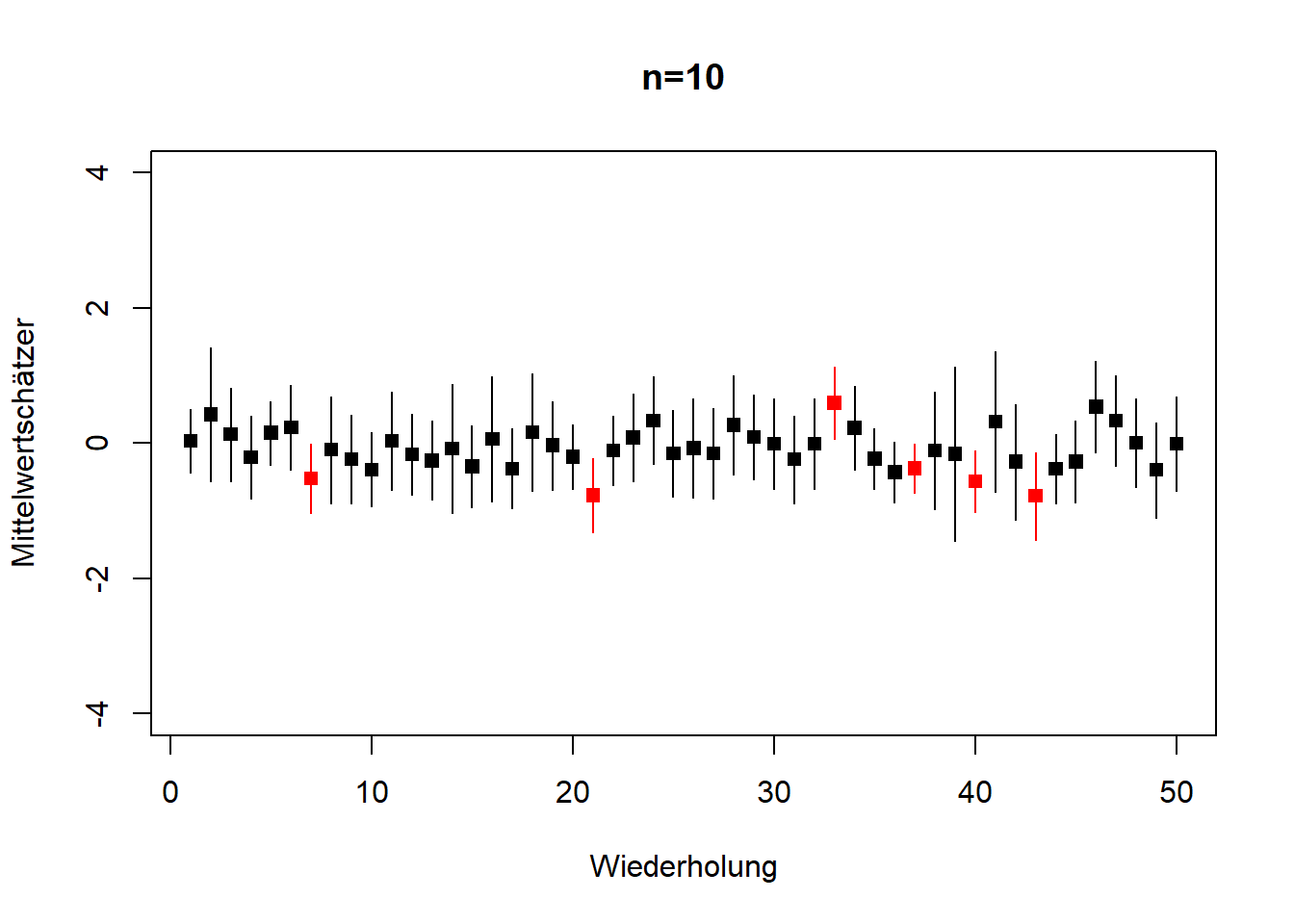
Abbildung 8.3: 50 Wiederholungen von Stichprobenziehungen aus der gleichen Grundgesamtheit, \(N(0,1)\), aus denen jeweils der Mittelwert geschätzt wurde, einmal mit \(n=5\) (links) und einmal mit \(n=10\) (rechts). Gezeigt ist jeweils der geschätzte Mittelwert mit Konfidenzintervall. Konfidenzintervalle, die den wahren Wert \(\mu=0\) nicht einschließen sind rot markiert; das sind bei einer ausreichenden Anzahl Wiederholungen 5%, d.h. in diesem Fall 2-3 von 50. Wenn hier die Grafiken abweichen dann liegt das an der geringen Anzahl Wiederholungen. Außerdem sehen wir, dass bei größerem Stichprobenumfang der Standardfehler und damit die Breite der Konfidenzintervalle kleiner sind (\(n=10\) rechts im Vergleich zu \(n=5\) links); vgl. Gleichung (8.5). Nach: Mittag (2016).
8.3 Normalverteilung: Schätzer für \(\sigma\)
Der Schätzer für \(\sigma\) ist: \[\begin{equation} \hat\sigma=s=\sqrt{\frac{\sum_{i=1}^{n}\left(x_i-\bar x\right)^2}{n-1}} \tag{8.13} \end{equation}\]
In Worten: Der Schätzer der Standardabweichung einer normalverteilten Grundgesamheit \(\hat\sigma\) ist die Standardabweichung einer Stichprobe aus dieser Grundgesamtheit.
Die Herleitung beider Schätzer erfolgt über die sogenannte Maximum-Likelihood-Theorie, auf die wir hier nicht näher eingehen wollen. Sie können die Herleitung aber z.B. in Dormann (2013), S. 48ff nachlesen. Auf der Maximum-Likelihood-Theorie basiert die Annahme unabhängig identisch verteilter (u.i.v.) Daten. Nur wenn diese erfüllt ist, sind die o.g. wahrscheinlichkeitstheoretische Aussagen wie Standardfehler und Konfidenzintervalle gültig! Oft, z.B. wenn Daten korrelieren, ist dies nur annäherungsweise der Fall und wir müssen andere Formeln benutzen.
8.4 Quantil-Quantil-Diagramm (QQ-Plot)
Ein visueller Test, ob eine Stichprobe aus einer bestimmten Verteilung entstammt ist das sogenannte Quantil-Quantil-Diagramm (QQ-Plot). Abbildung 8.4 zeigt QQ-Plots für unsere Entfernungsdaten, einmal original und einmal log-transformiert.
# QQ-Plot für Originaldaten
qqnorm(reisedat$distanz)
qqline(reisedat$distanz)
# QQ-Plot für log-transformierte Daten
qqnorm(log(reisedat$distanz))
qqline(log(reisedat$distanz))). Eine Lognormalverteilung passte hier mässig gut. Rechts: QQ-Plot der log-transformierten Entfernungsdaten. Die Verteilung der transformierten Daten hat flachere Flanken als eine Normalverteilung ("heavier tails"), was sich an der Form der Kurve zeigt (vgl. [QQ-Plot App](https://xiongge.shinyapps.io/QQplots/)).](eids_files/figure-html/qqentfernung-1.png)
). Eine Lognormalverteilung passte hier mässig gut. Rechts: QQ-Plot der log-transformierten Entfernungsdaten. Die Verteilung der transformierten Daten hat flachere Flanken als eine Normalverteilung ("heavier tails"), was sich an der Form der Kurve zeigt (vgl. [QQ-Plot App](https://xiongge.shinyapps.io/QQplots/)).](eids_files/figure-html/qqentfernung-2.png)
Abbildung 8.4: Links: QQ-Plot der Entfernungsdaten. Wie wir in Kapitel 3 und Kapitel 7 gesehen haben sind die Originaldaten rechtsschief (“right-skewed”), was wir an dem nach oben gewölbten QQ-Plot sehen (vgl. QQ-Plot App). Eine Lognormalverteilung passte hier mässig gut. Rechts: QQ-Plot der log-transformierten Entfernungsdaten. Die Verteilung der transformierten Daten hat flachere Flanken als eine Normalverteilung (“heavier tails”), was sich an der Form der Kurve zeigt (vgl. QQ-Plot App).
Im QQ-Plot stellt jeder Datenpunkt ein bestimmtes Quantil der empirischen Verteilung dar (vgl. Kapitel 3). Dieses Quantil (nach Standardisierung; vgl. Kapitel 4) wird gegen den Wert dieses Quantils geplotted (vertikale Achse), der unter einer Standard-Normalverteilung (horizontale Achse) erwartet wird. Die resultierenden Formen sagen etwas über die Verteilung aus. Dies veranschaulicht diese QQ-Plot App ganz schön. Im Fall einer Normalverteilung fallen alle Punkte auf eine gerade Linie.