Kapitel 10 Lineare Regression
Für die lineare Regression kehren wir zunächst zu einer Frage aus Kapitel 5 zurück: Kann man Ihre Anreisezeit nach Adlershof mit der Entfernung zu Ihrem Wohnort statistisch vorhersagen?
plot(reisedat$distanz, reisedat$zeit_morgens,
xlab = "Entfernung (km)", ylab = "Reisezeit, morgens (min)")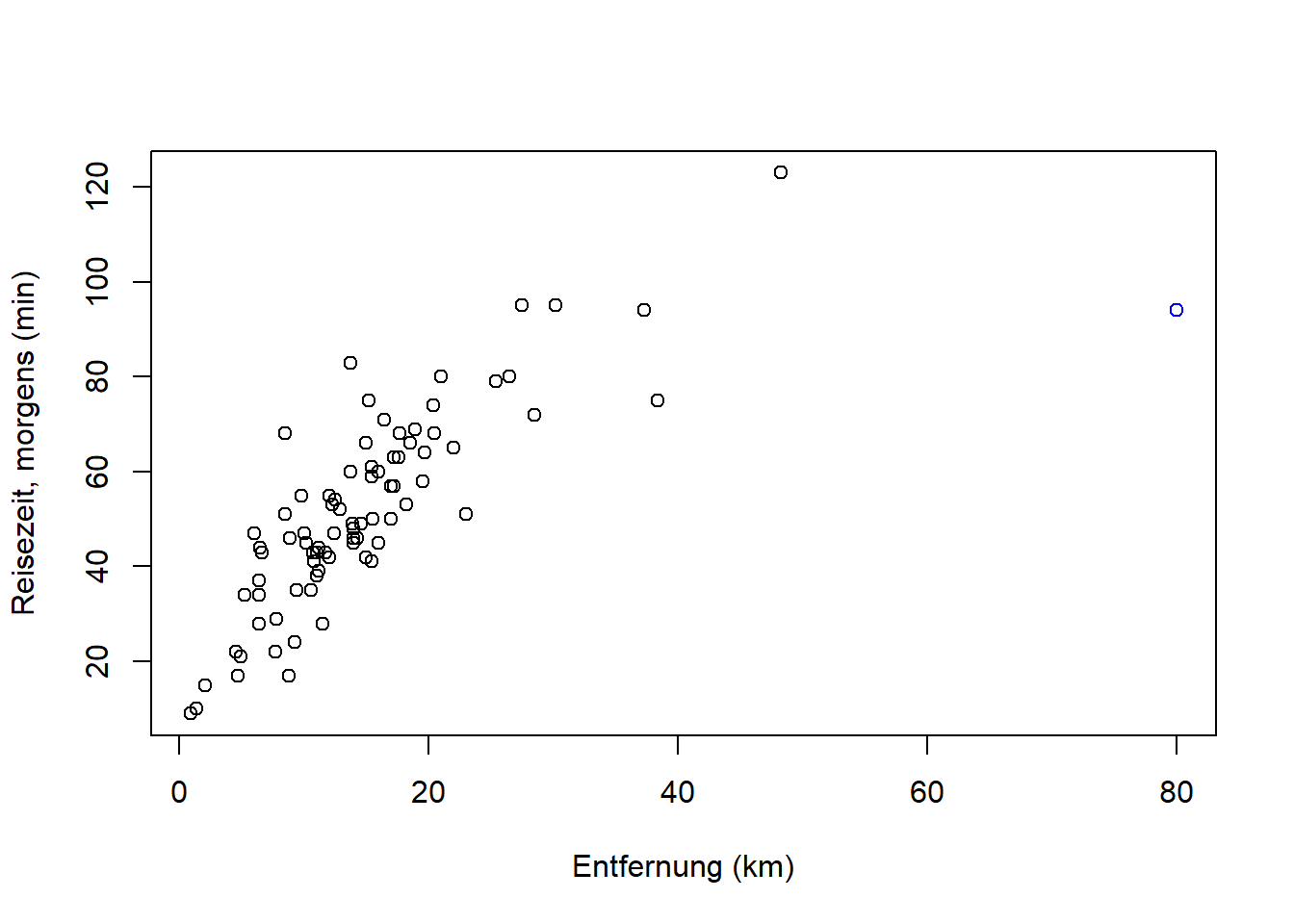
Wir erinnern uns, dass der Korrelationskoeffizient nach Bravais-Pearson aus Kapitel 5 0.72 war, wenn wir den Punkt oben rechts rauslassen, dann 0.78. Das Ziel ist nun, eine Gerade durch die Punktwolke zu legen, die den Trend beschreibt, so dass der Abstand der Punkte von der Geraden minimal ist.
Es geht um 2 Variablen (Merkmale):
- die abhängige Variable \(y\) (im Bsp. Reisezeit)
- die unabhängige Variable \(x\) (im Bsp. Entfernung)
Die Variablen müssen metrisch skaliert sein. Das ist korrekt wenn wir von linearer Regression im engen Sinn sprechen, obwohl Regressionsprobleme mit nominal oder ordinal skalierten unabhängigen Variablen mathematisch identisch sind. Das werden wir weiter unten, in Kapitel 10.8, noch sehen. 22 In jedem Fall wollen wir das generelle Verhalten von \(y\) mit \(x\) beschreiben. Eine Gerade stellt dabei das einfachste lineare Modell dar.
10.1 Definitionen
Im Fall einer einzigen unabhängigen Variable lautet die Gleichung des linearen Models:
\[\begin{equation} y_i = \beta_0 + \beta_1 \cdot x_i + \epsilon_i \quad \text{mit} \quad i=1,2,\ldots,n \tag{10.1} \end{equation}\]
\(y_i\) bezeichnet den Wert der abhängigen Variable für Datenpunkt \(i\) und \(x_i\) den Wert der unabhängigen Variable für Datenpunkt \(i\). Der Parameter \(\beta_0\) beschreibt den Achsenabschnitt der Geraden, also der Punkt, an dem die Gerade die y-Achse schneidet. Der Parameter \(\beta_1\) beschreibt die Steigung der Geraden. \(\epsilon_i\) stellt das Residuum (man sagt auch Fehler) für Datenpunkt \(i\) dar (Abbildung 10.1).
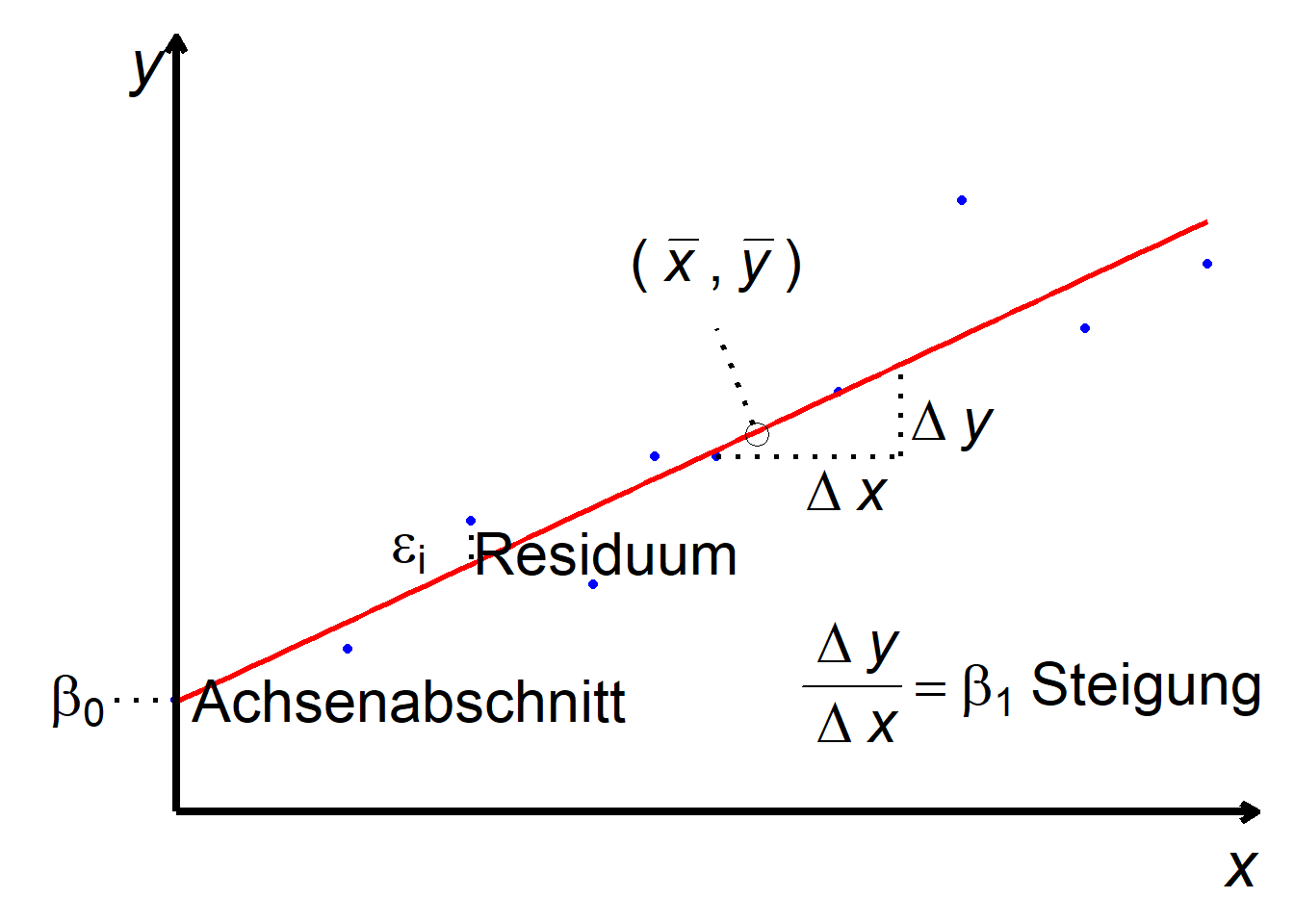
Abbildung 10.1: Lineare Regression: Definitionen.
10.2 Beschreibung vs. Vorhersage
Der primäre Zweck einer Regressionsanalyse ist die Beschreibung (oder Erklärung) der Daten im Sinn einer allgemeinen Beziehung, die sich auf die Grundgesamtheit übertragen lässt, aus der diese Daten entnommen wurden. Da diese Beziehung eine Eigenschaft der Grundgesamtheit ist, sollte sie auch Vorhersagen ermöglichen. Hierbei ist jedoch Vorsicht geboten. Betrachten Sie den Zusammenhang von Jahr und Weltrekordzeit für die in Abbildung 10.2 dargestellten Daten (“Meile, Herren”). Wenn, wie hier, die Zeit die unabhängige Variable ist, wird die Regression zu einer Form der Trendanalyse, die in diesem Fall eine Abnahme der Rekordzeit mit den Jahren anzeigt. (Die lm() Funktion und ihre Ausgaben werden wir weiter unten kennenlernen, hier geht es um die Grafiken.)
# Daten laden
mile <- read.csv("https://raw.githubusercontent.com/avehtari/ROS-Examples/master/Mile/data/mile.csv", header=TRUE)
# lineares Modell an Daten aus 1. Hälfte des 20. Jahrh. anpassen
mile_fit1 <- lm(seconds ~ year, data = mile[mile$year<1950,])
# Informationen zu Parameterschätzern extrahieren
coef(summary(mile_fit1))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 912.2340 67.90140 13.435 3.615e-08
## year -0.3439 0.03509 -9.798 9.059e-07# lineares Modell an kompletten Datensatz anpassen
mile_fit2 <- lm(seconds ~ year, data = mile)
coef(summary(mile_fit2))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1006.876 21.532 46.76 1.361e-29
## year -0.393 0.011 -35.73 3.780e-26# Modellanpassung für 1. Hälfte des 20. Jahrh. plotten
plot(mile$year[mile$year<1950], mile$seconds[mile$year<1950],
xlim = c(1900, 2000), ylim = c(200, 260),
pch = 19, type = 'p',
xlab = "Jahr", ylab = "Weltrekord, Meile, Herren (Sekunden)")
abline(coef(mile_fit1), lwd = 3, col = "red")
# Extrapolation für 2. Hälfte des 20. Jahrh. plotten
plot(mile$year, mile$seconds,
xlim = c(1900, 2000), ylim = c(200, 260),
pch = 19, type = 'p',
xlab = "Jahr", ylab = "Weltrekord, Meile, Herren (Sekunden)")
abline(coef(mile_fit1), lwd = 3, col = "red")
# Modellanpassung für Gesamtdaten bis 2050 plotten
plot(mile$year, mile$seconds,
xlim = c(1900, 2050), ylim = c(200, 260),
pch = 19, type = 'p',
xlab = "Jahr", ylab = "Weltrekord, Meile, Herren (Sekunden)")
abline(coef(mile_fit2), lwd = 3, col = "red")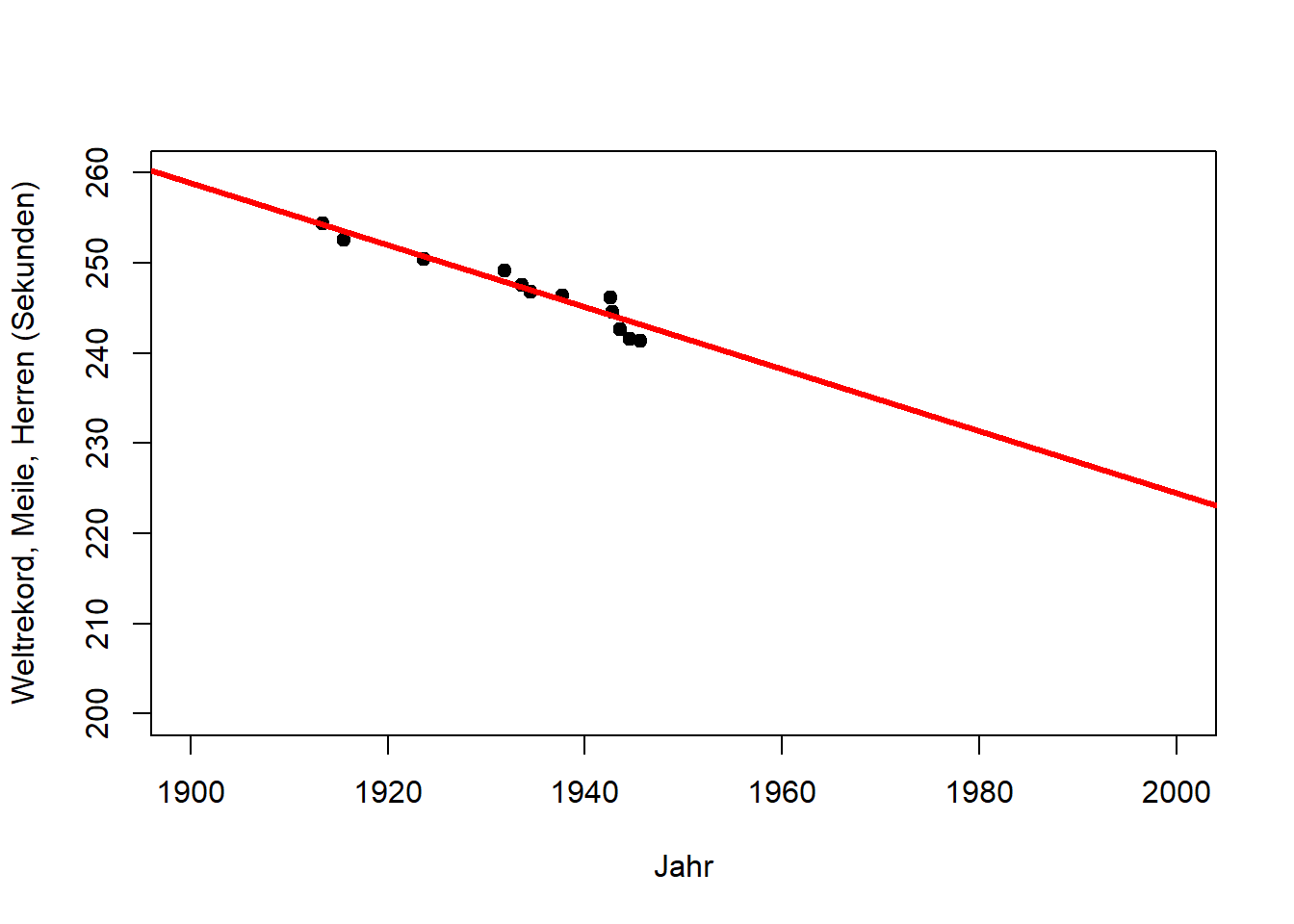
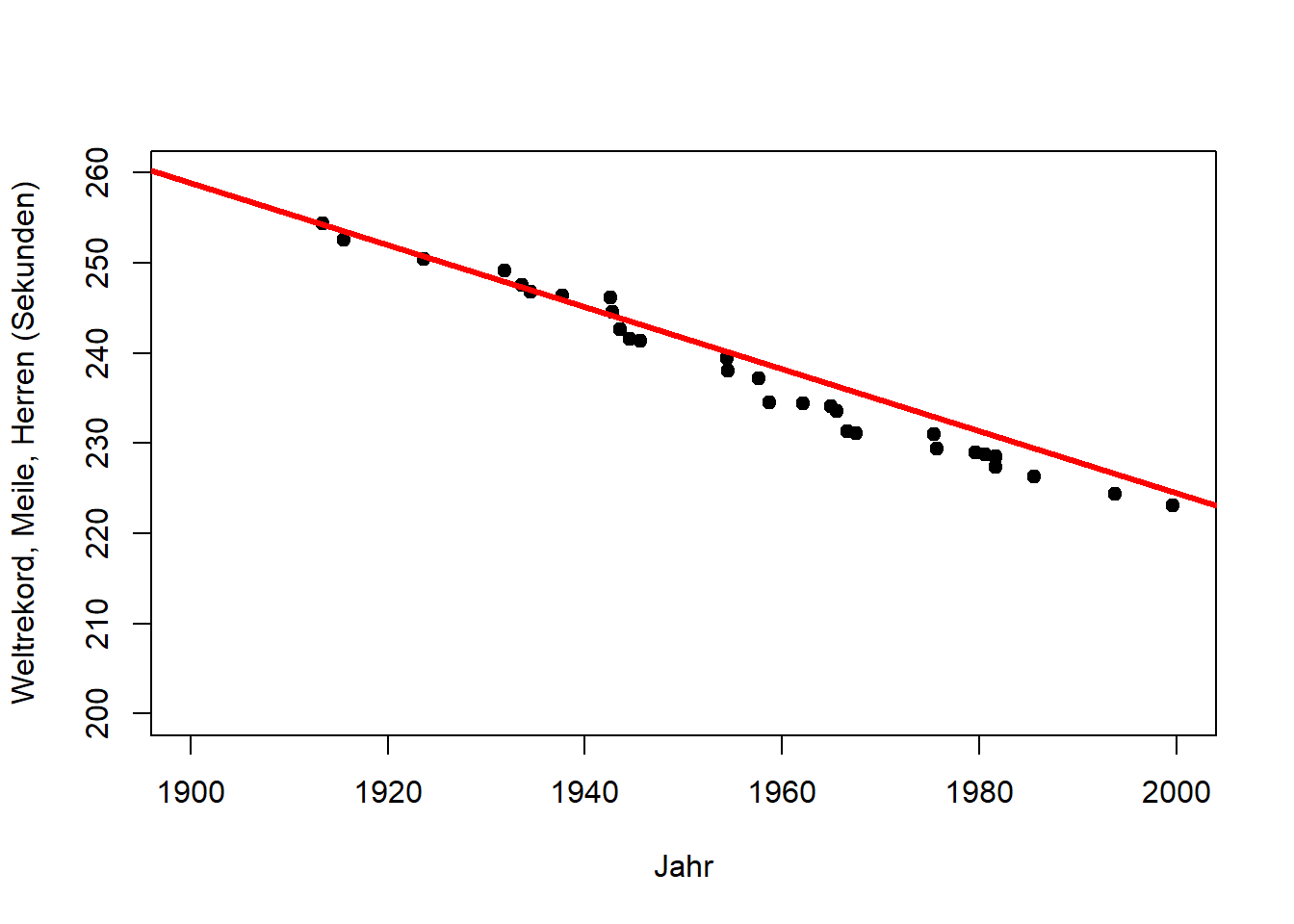
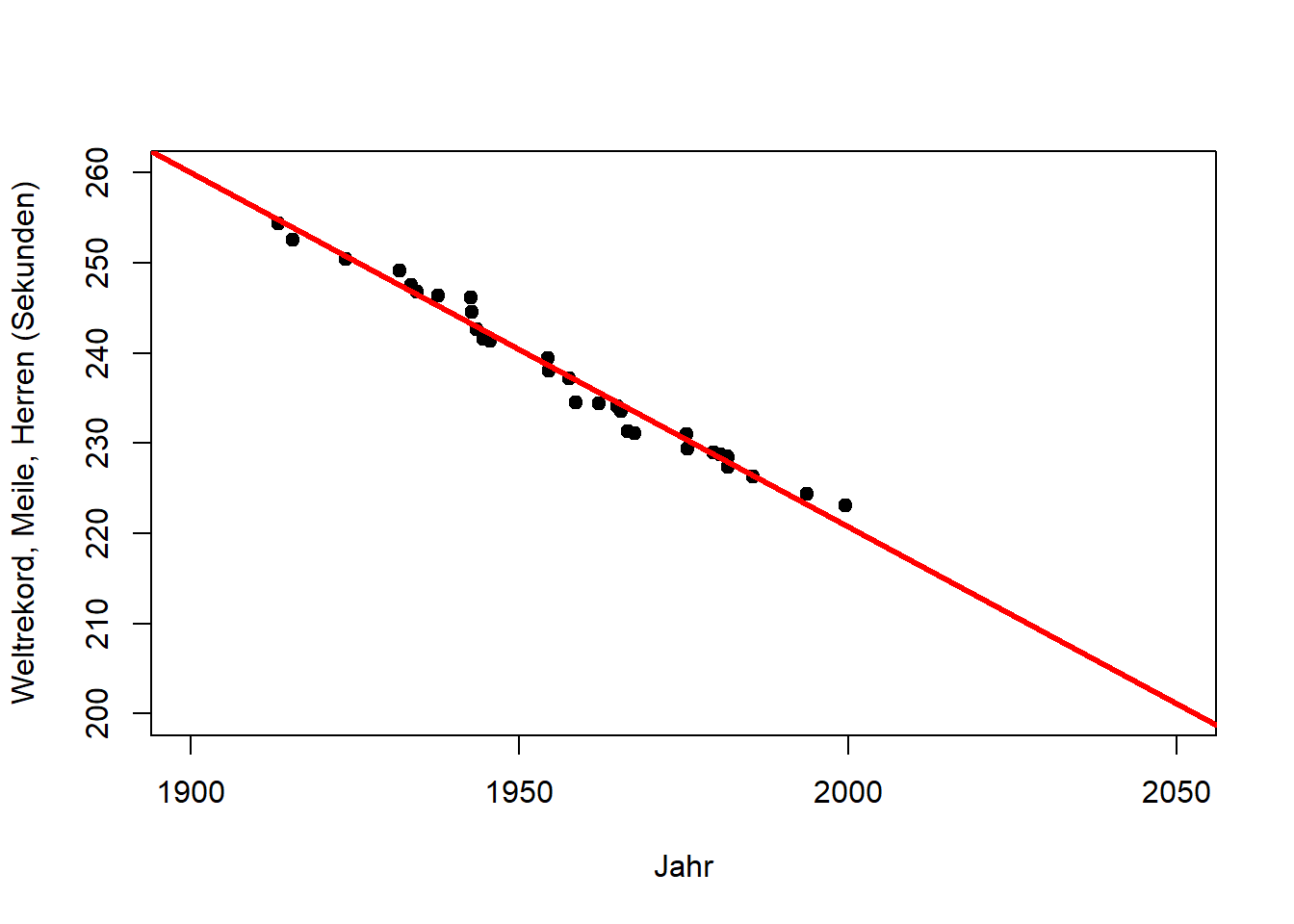
Abbildung 10.2: Links: Trend des Weltrekords Meile, Herren in der ersten Hälfte des 20. Jahrhunderts (Beschreibung). Mitte: Extrapolation des Trends für die zweite Hälfte des 20. Jahrhunderts (Vorhersage). Rechts: Extrapolation des Trends bis zum Jahr 2050 (längere Vorhersage). Nach: Wainer (2009)
Wir sehen, dass sich der Weltrekord in der ersten Hälfte des 20. Jahrhunderts linear verbesserte (Abbildung 10.2, links). Dieser Trend passt auch für die zweite Hälfte des 20. Jahrhunderts bemerkenswert gut (Abbildung 10.2, Mitte). Wie lange kann sich der Weltrekord jedoch noch mit der gleichen Rate verbessern (Abbildung 10.2, rechts)?
Dieses Beispiel zeigt deutlich die Anwendbarkeit von Regressionen für Vorhersagen, zeigt jedoch gleichzeitig die Grenzen dieser einfachen Modelle für längere Vorhersagen (z.B. in Zeit und Raum). Im Fall des Weltrekords würden wir erwarten, dass die Verbesserungsrate mit der Zeit abnimmt, d.h. dass die Kurve abflacht, was ein nichtlineares Modell erfordert.
10.3 Ausblick: Weiterführende lineare Modelle
Wenn wir über das lineare Modell sprechen, ist die abhängige Variable immer metrisch skaliert, während die unabhängigen Variablen metrisch, nominal/ordinal oder gemischt sein können. Im Prinzip kann jede dieser Varianten mathematisch gleich behandelt werden, d.h. alle können z.B. mit der lm() Funktion in R analysiert werden. Allerdings haben sich historisch gesehen unterschiedliche Bezeichnungen für diese Varianten etabliert, die hier erwähnt werden sollen, um Verwirrung zu vermeiden (Tabellen 10.1 und 10.2). Wie Sie sehen, kann auch die Varianzanalyse (ANOVA) aus Kapitel 9.5 als ein Spezialfall des linearen Modells verstanden werden, worauf wir weiter unten in Kapitel 10.8 noch eingehen werden.
| unabhängige Variable(n) metrisch |
unabhängige Variable(n) nominal/ordinal |
unabhängige Variable(n) gemischt |
|---|---|---|
| Regression | Varianzanalyse (ANOVA) |
Kovarianzanalyse (ANCOVA) |
| 1 unabhängige Variable | >1 unabhängige Variable | |
|---|---|---|
| 1 abhängige Variable | Regression | Multiple Regression |
| >1 abhängige Variable | Multivariate Regression | Multivariate multiple Regression |
10.4 Lineare Regression
Erstmal zurück zur linearen Regression im engen Sinn. Wie soll die Gerade durch die Punktwolke gelegt werden, d.h. welche Werte sollen Achsenabschnitt \(\beta_0\) und Steigung \(\beta_1\) annehmen? Typischerweise werden Regressionsprobleme gelöst, indem die Summe der quadratischen Abweichungen zwischen der Regressionsgeraden und den Datenpunkten minimiert wird - die sogenannte Kleinste-Quadrate-Schätzung. Die Summe der quadratischen Abweichungen kennen wir schon von der Definition der Varianz (Kapitel 4) und von der ANOVA (Kapitel 9.5).
Die Summe der quadratischen Abweichungen wird wie gesagt als \(SSE\) bezeichnet (Sum of Squared Errors). Grafisch gesehen probieren wir in Abbildung 10.1 verschiedene Geraden mit unterschiedlichen Achsenabschnitten \(\beta_0\) und Steigungen \(\beta_1\) aus und wählen diejenige, bei der die Summe aller vertikalen Abstände \(\epsilon_i\) zum Quadrat am kleinsten ist. Mathematisch ist \(SSE\) in diesem Fall:
\[\begin{equation} SSE=\sum_{i=1}^{n}\left(\epsilon_i\right)^2=\sum_{i=1}^{n}\left(y_i-\left(\beta_0+\beta_1 \cdot x_i\right)\right)^2 \tag{10.2} \end{equation}\]
Das Residuum \(\epsilon_i\) ist also gleich \(y_i-\left(\beta_0+\beta_1 \cdot x_i\right)\), dem vertikalen Abstand zwischen Datenpunkt und Regressionsgerade.
Im Fall der linearen Regression kann \(SSE\) analytisch minimiert werden, was z.B. bei nichtlinearen Modellen nicht der Fall ist. Analytisch finden wir das Minimum von \(SSE\) wo dessen partielle Ableitungen in Bezug auf die beiden Modellparameter beide Null sind: \(\frac{\partial SSE}{\partial \beta_0}=0\) und \(\frac{\partial SSE}{\partial \beta_1}=0\). Unter Anwendung der Definition von \(SEE\) aus Gleichung (10.2) und der Summenregel23 und der Kettenregel24, die Sie noch aus der Schule kennen werden, erhalten wir:
\[\begin{equation} \frac{\partial SSE}{\partial \beta_0}=-2 \cdot \sum_{i=1}^{n}\left(y_i-\beta_0-\beta_1 \cdot x_i\right)=0 \tag{10.3} \end{equation}\] \[\begin{equation} \frac{\partial SSE}{\partial \beta_1}=-2 \cdot \sum_{i=1}^{n}x_i \cdot \left(y_i-\beta_0-\beta_1 \cdot x_i\right)=0 \tag{10.4} \end{equation}\]
Gleichungen (10.3) und (10.4) bilden ein Gleichungssystem mit zwei Gleichungen und zwei Unbekannten, das wir eindeutig lösen können. Zuerst lösen wir Gleichung (10.3) nach \(\beta_0\) auf (nachdem wir durch -2 geteilt haben):
\[\begin{equation} \sum_{i=1}^{n}y_i-n \cdot \beta_0-\beta_1 \cdot \sum_{i=1}^{n}x_i=0 \tag{10.5} \end{equation}\] \[\begin{equation} n \cdot \beta_0=\sum_{i=1}^{n}y_i-\beta_1 \cdot \sum_{i=1}^{n}x_i \tag{10.6} \end{equation}\] \[\begin{equation} \beta_0=\bar{y}-\beta_1 \cdot \bar{x} \tag{10.7} \end{equation}\]
Formal sind das jetzt Parameterschätzer (das “Dach”-Symbol bezeichnet Schätzer): \[\begin{equation} \hat\beta_0=\bar{y}-\hat\beta_1 \cdot \bar{x} \tag{10.8} \end{equation}\]
Sodann setzen wir Gleichung (10.8) in Gleichung (10.4) ein (nachdem wir durch -2 geteilt haben):
\[\begin{equation} \sum_{i=1}^{n}\left(x_i \cdot y_i-\beta_0 \cdot x_i-\beta_1 \cdot x_i^2\right)=0 \tag{10.9} \end{equation}\] \[\begin{equation} \sum_{i=1}^{n}\left(x_i \cdot y_i-\bar{y} \cdot x_i+\hat\beta_1 \cdot \bar{x} \cdot x_i-\hat\beta_1 \cdot x_i^2\right)=0 \tag{10.10} \end{equation}\]
Schließlich lösen wir Gleichung (10.10) nach \(\beta_1\) auf:
\[\begin{equation} \sum_{i=1}^{n}\left(x_i \cdot y_i-\bar{y} \cdot x_i\right)-\hat\beta_1 \cdot \sum_{i=1}^{n}\left(x_i^2-\bar{x} \cdot x_i\right)=0 \tag{10.11} \end{equation}\] \[\begin{equation} \hat\beta_1=\frac{\sum_{i=1}^{n}\left(x_i \cdot y_i-\bar{y} \cdot x_i\right)}{\sum_{i=1}^{n}\left(x_i^2-\bar{x} \cdot x_i\right)} \tag{10.12} \end{equation}\]
Über eine Reihe von Umformungen, die ich hier überspringe, erhalten wir:
\[\begin{equation} \hat\beta_1=\frac{SSXY}{SSX} \tag{10.13} \end{equation}\]
\(SSX=\sum_{i=1}^{n}\left(x_i-\bar{x}\right)^2\) ist ein Maß für die Varianz der Daten in \(x\)-Richtung. \(SSXY=\sum_{i=1}^{n}\left(x_i-\bar{x}\right) \cdot \left(y_i-\bar{y}\right)\) ist ein Maß für die Kovarianz der Daten. In Kapitel 9.5 hatten wir noch \(SSY=\sum_{i=1}^{n}\left(y_i-\bar{y}\right)^2\), das entsprechend ein Maß für die Varianz der Daten in \(y\)-Richtung ist. Gleichung (10.13) ist eine exakte Lösung für \(\hat\beta_1\).
Wir setzen nun Gleichung (10.13) in Gleichung (10.8) ein und haben eine exakte Lösung für \(\hat\beta_0\). Berechnen wir nun die Parameter für unsere Reisedaten mit der lm() Funktion:
# lineare Regression der Reisedaten
reise_fit <- lm(zeit_morgens ~ distanz, data = reisedat)
# Informationen über geschätzte Parameterwerte ausgeben
coef(summary(reise_fit))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 29.080 3.2687 8.897 1.282e-12
## distanz 1.588 0.1934 8.207 1.936e-11In der ersten Spalte (“Estimate”) dieses Outputs finden Sie die Werte der Parameterschätzer, wobei “(Intercept)” für \(\beta_0\) steht und “distanz” (in diesem Fall) für \(\beta_1\). Anhand von \(\beta_1\) können wir ablesen, dass sich pro km Entfernung die Reisezeit um 1.6min erhöht. Der Achsenabschnitt \(\beta_0\) hat keine direkte Entsprechung.25 Auf die anderen Spalten werden wir weiter unten zu sprechen kommen. Plotten wir nun die so ermittelte Regressionsgerade \(y_i=29.1+1.6\cdot x_i+\epsilon_i\):
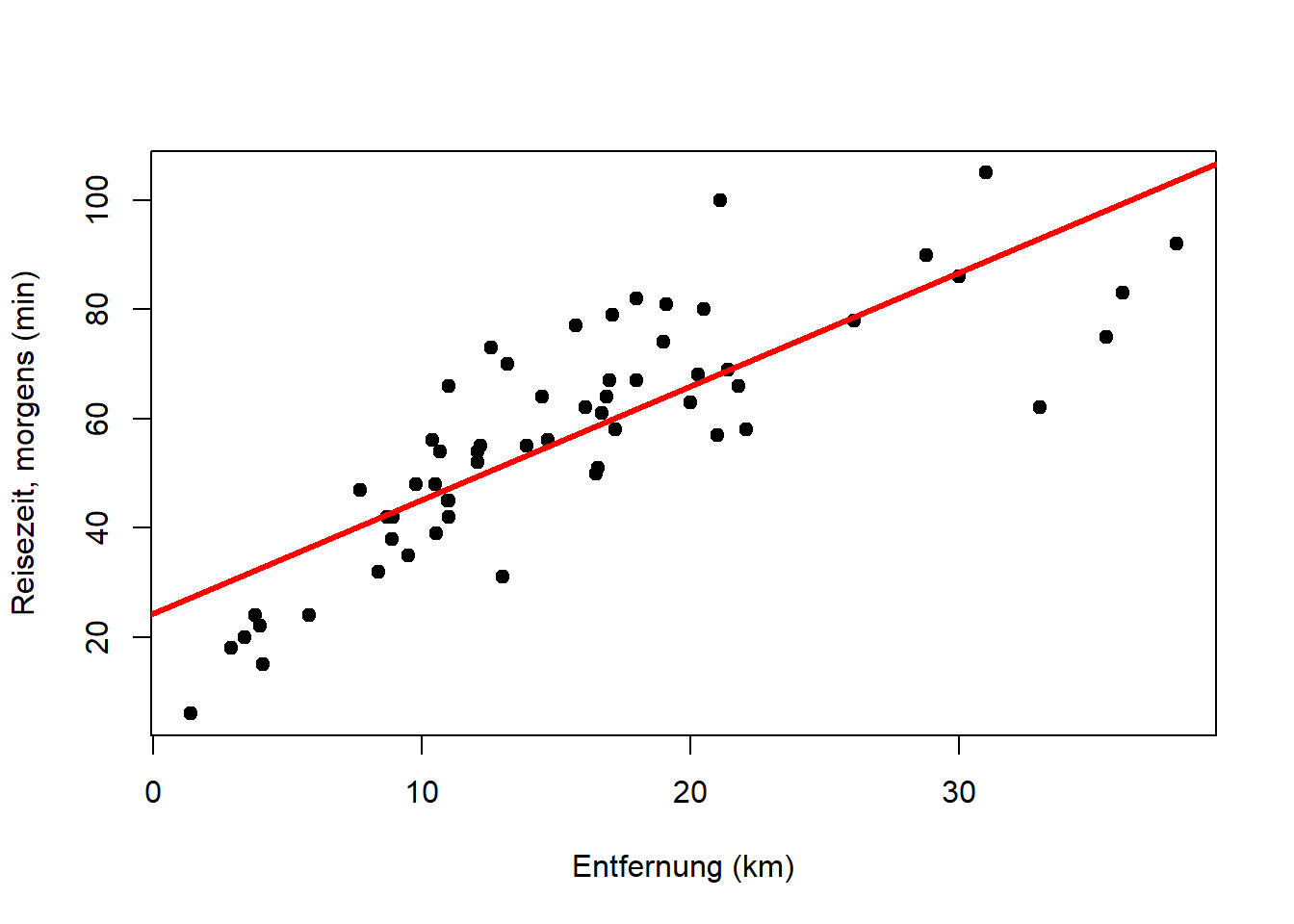
In Kapitel 5 haben wir bereits gesehen, dass der Zusammenhang durch den Punkt ganz rechts nicht-linear wird, da vermutlich mit zunehmender Entfernung die gewählten Verkehrsmittel effizienter werden (kürzere Reisezeit pro km). Vergleichen wir also die Regression mit einer Variante ohne den Punkt ganz rechts:
# Zeitreihe ohne statistische Einheit Nr. 6
reisedat2 <- reisedat[-6,]
# lineare Regression
reise_fit2 <- lm(zeit_morgens ~ distanz, data = reisedat2)
# Informationen über geschätzte Parameterwerte ausgeben
coef(summary(reise_fit2))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 21.53 3.4700 6.205 5.568e-08
## distanz 2.19 0.2285 9.584 1.040e-13# Modellanpassung plotten
plot(reisedat2$distanz, reisedat2$zeit_morgens,
pch = 19, type = 'p', xlab = "Entfernung (km)", ylab = "Reisezeit, morgens (min)")
abline(coef(reise_fit2), lwd = 3, col = "red")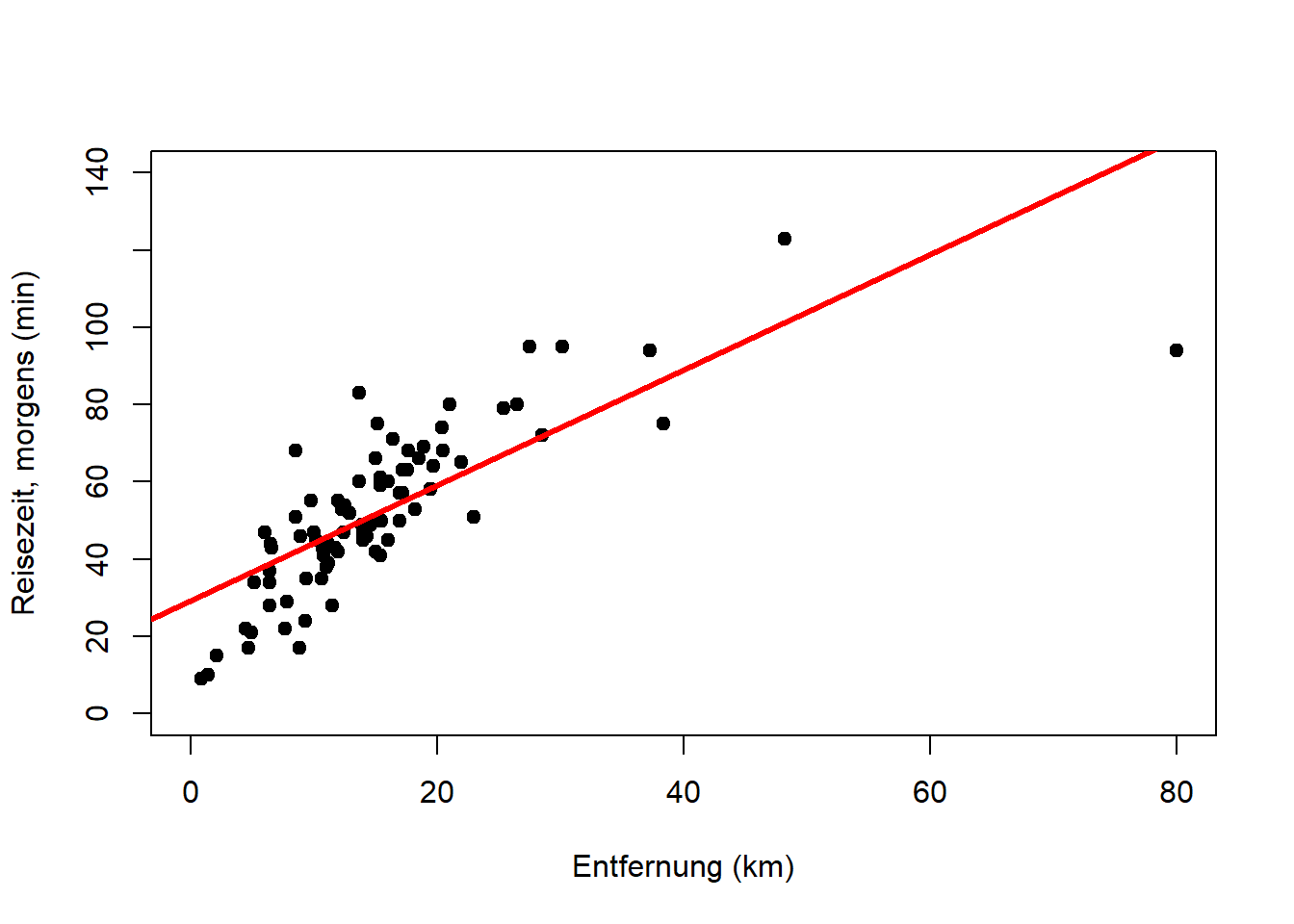
Das lineare Modell passt hier viel besser. Die Steigung ist jetzt 2.2min pro km und der Achsenabschnitt 21.5min. Wir rechnen im Folgenden mit diesem Modell weiter, das aber wohlgemerkt nur ein Modell für Entfernungen bis ca. 40km ist. Darüber hinaus wird der Zusammenhang nicht-linear.
10.5 Erklärte Varianz
Nun, da wir Werte für die Regressionsparameter haben, testen wir üblicherweise formal, ob die vom Modell erklärte Varianz in den Daten größer als die nicht erklärte Varianz ist (bezogen auf die Grundgesamtheit). Das ist ein ANOVA-Problem (Kapitel 9.5). Die ANOVA-Tabelle (in diesem Fall Tabelle 10.3) wird in R im Hintergrund aufgestellt und selten explizit betrachtet; tun wir es hier aber trotzdem, damit wir verstehen, was passiert.
| Varianz- quelle |
Quadrat- summe |
Freiheits- grad (\(df\)) |
Varianz | F-Statistik (\(F_s\)) | p-Wert |
|---|---|---|---|---|---|
| Regression | \(SSR=\\SSY-SSE\) | \(1\) | \(\frac{SSR}{df_{SSR}}\) | \(\frac{\frac{SSR}{df_{SSR}}}{s^2}\) | \(1-F\left(F_s,1,n-2\right)\) |
| Residuum | \(SSE\) | \(n-2\) | \(\frac{SSE}{df_{SSE}}=s^2\) | ||
| Gesamt | \(SSY\) | \(n-1\) |
Analog zur ANOVA-Tabelle aus Kapitel 9.5 (Tabelle 9.1), ist \(SSY=\sum_{i=1}^{n}\left(y_i-\bar{y}\right)^2\) ein Maß für die Gesamtvarianz der Daten (in \(y\)-Richtung), d.h. wie stark die Datenpunkte um den Gesamtmittelwert streuen (Abbildung 10.3, links). \(SSE=\sum_{i=1}^{n}\left(\epsilon_i\right)^2=\sum_{i=1}^{n}\left(y_i-\left(\beta_0+\beta_1 \cdot x_i\right)\right)^2\) ist ein Maß für die Fehlervarianz, d.h. wie stark die Datenpunkte um die Regressionsgerade streuen (Abbildung 10.3, rechts). Das ist die Varianz, die nach der Modellanpassung übrig ist (“nicht erklärt”). \(SSR=SSY-SSE\) ist folglich ein Maß für die vom Modell erklärte Varianz. Im Fall der ANOVA in Kapitel 9.5 sprechen wir von \(SSA\); das Modell ist dann der “Faktor” (kategorische Variable).
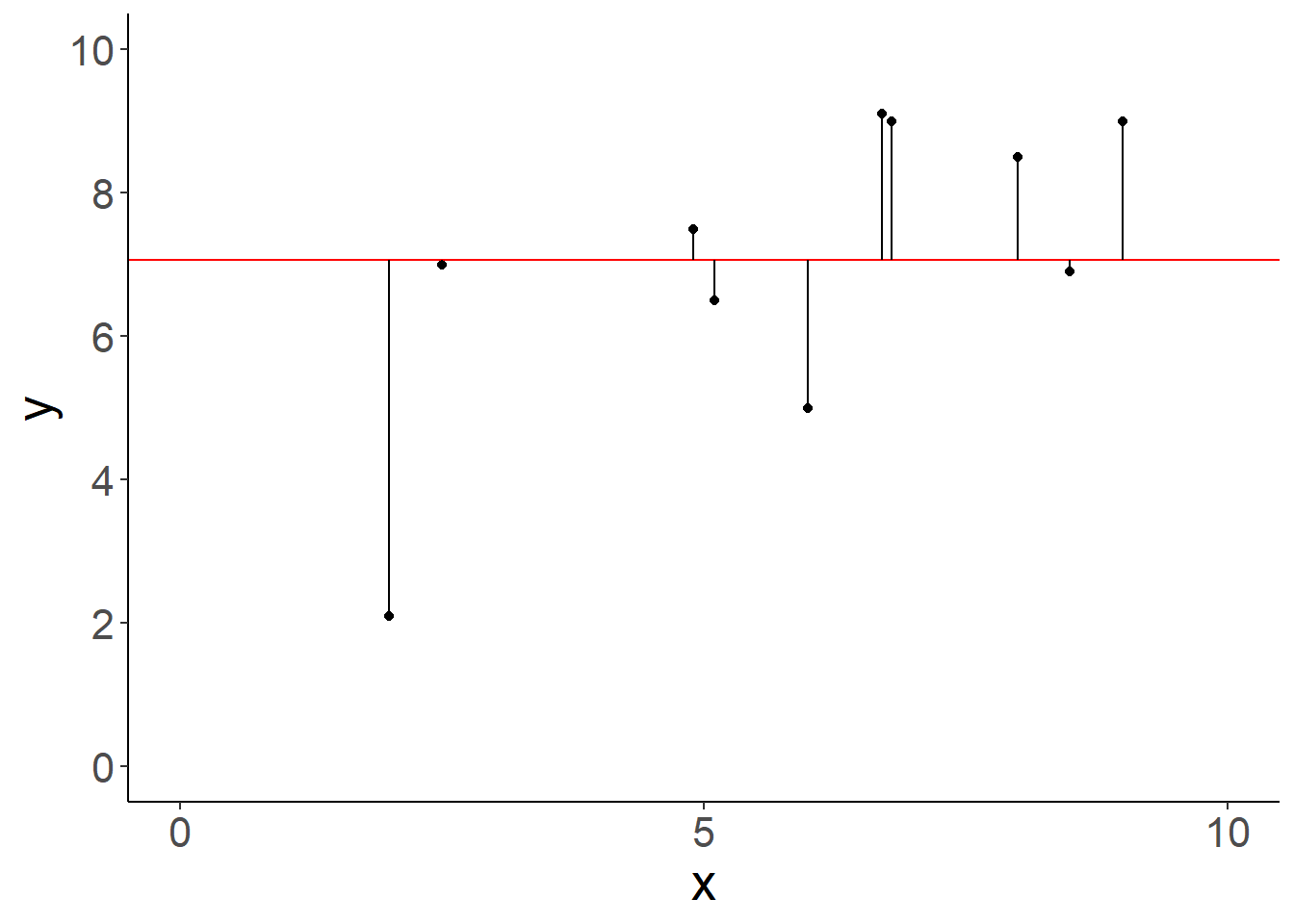
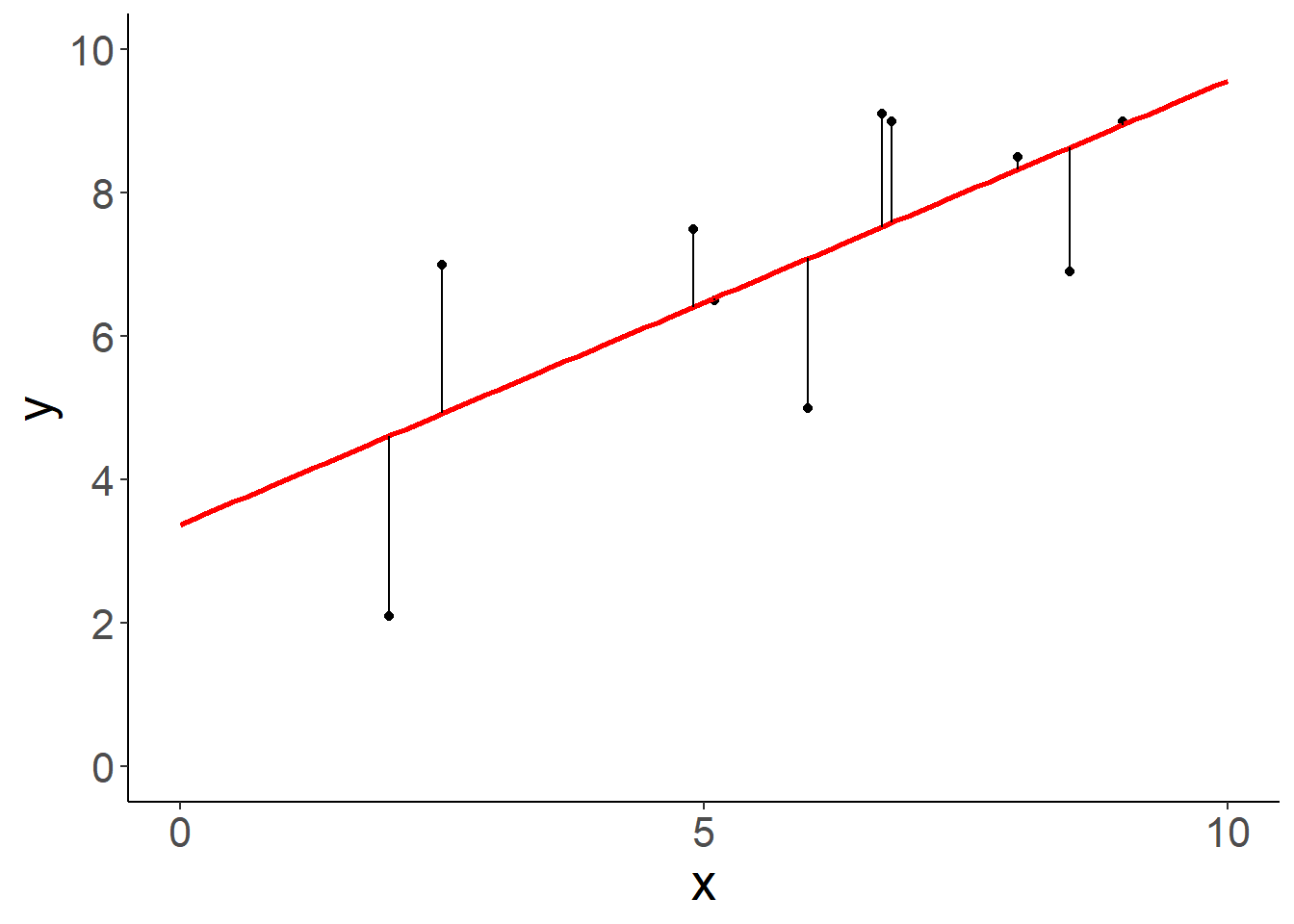
Abbildung 10.3: Variation der Datenpunkte um den Mittelwert, zusammengefasst durch \(SSY\) (links), und um die Regressionsgerade, zusammengefasst durch \(SSE\) (rechts).
In der dritten Spalte der Tabelle 10.3 stehen die Freiheitsgrade der drei Varianzterme. Diese können wie gehabt als Anzahl der Werte in einer Stichprobe, die für die Berechnung der jeweiligen Parameter frei zur Verfügung stehen, verstanden werden (vgl. Kapitel 4 und Kapitel 9.5): In die Berechnung von \(SSY\) geht \(\bar y\) ein, für dessen Berechnung die Werte der Stichprobe bereits einmal verwendet wurden; dadurch ist die Anzahl Freiheitsgrade \(df_{SSY}=n-1\). In die Berechnung von \(SSE\) gehen \(\beta_0\) und \(\beta_1\) ein (Gleichung (10.2)), d.h. die Anzahl Freiheitsgrade ist \(df_{SSE}=n-2\). Für \(SSR\) gilt dann einfach \(df_{SSR}=df_{SSY}-df_{SSE}=1\). Die Freiheitsgrade werden verwendet, um die Varianzterme in der vierten Spalte der Tabelle 10.3 zu normalisieren, d.h. auf die Skala einer Varianz zu bringen, wobei \(s^2\) Fehlervarianz genannt wird.
In der fünften Spalte der Tabelle 10.3 finden wir das Verhältnis von zwei Varianzen; Regressionsvarianz über Fehlervarianz. Von einer aussagekräftigen Regression erwarten wir, dass die (durch das Modell erklärte) Regressionsvarianz viel größer ist als die (durch das Modell nicht erklärte) Fehlervarianz. Dies ist ein F-Test Problem (vgl. Kapitel 9.5), bei dem getestet wird, ob sich die durch das Modell erklärte Varianz von der durch das Modell nicht erklärten Varianz (bezogen auf die Grundgesamtheit) unterscheidet. Das Verhältnis der beiden Varianzen dient als F-Statistik \(F_s\).
Die sechste Spalte der Tabelle 10.3 gibt dann den p-Wert des F-Tests an, d.h. die Wahrscheinlichkeit, \(F_s\) oder einen größeren Wert (d.h. ein noch besseres Modell) zufällig zu erhalten, wenn die Nullhypothese \(H_0\) wahr ist (vgl. Kapitel 9.5). Im Fall der linearen Regression ist \(H_0:\frac{SSR}{df_{SSR}}=s^2\), d.h. die beiden Varianzen sind gleich, und \(H_1:\frac{SSR}{df_{SSR}}>s^2\), d.h. die erklärte Varianz ist größer als die nicht erklärte.
Wie in Kapitel 9.4 bereits diskutiert, folgt \(F_s\) einer F-Verteilung unter der Nullhypothese, hier mit den Parametern \(1\) und \(n-2\) (Abbildung 10.4). Die blaue Linie in Abbildung 10.4 markiert einen bestimmten Wert von \(F_s\) (in diesem Beispiel \(8\)) und den entsprechenden Wert der Verteilungsfunktion der F-Verteilung (\(F\left(F_s,1,n-2\right)\)). Der p-Wert ist \(\Pr\left(Z> F_s\right)=1-F\left(F_s,1,n-2\right)\) und beschreibt die Wahrscheinlichkeit, dieses oder ein größeres Varianzverhältnis zufällig (aufgrund der zufälligen Stichprobenziehung) zu erhalten, selbst wenn die beiden Varianzen tatsächlich gleich sind.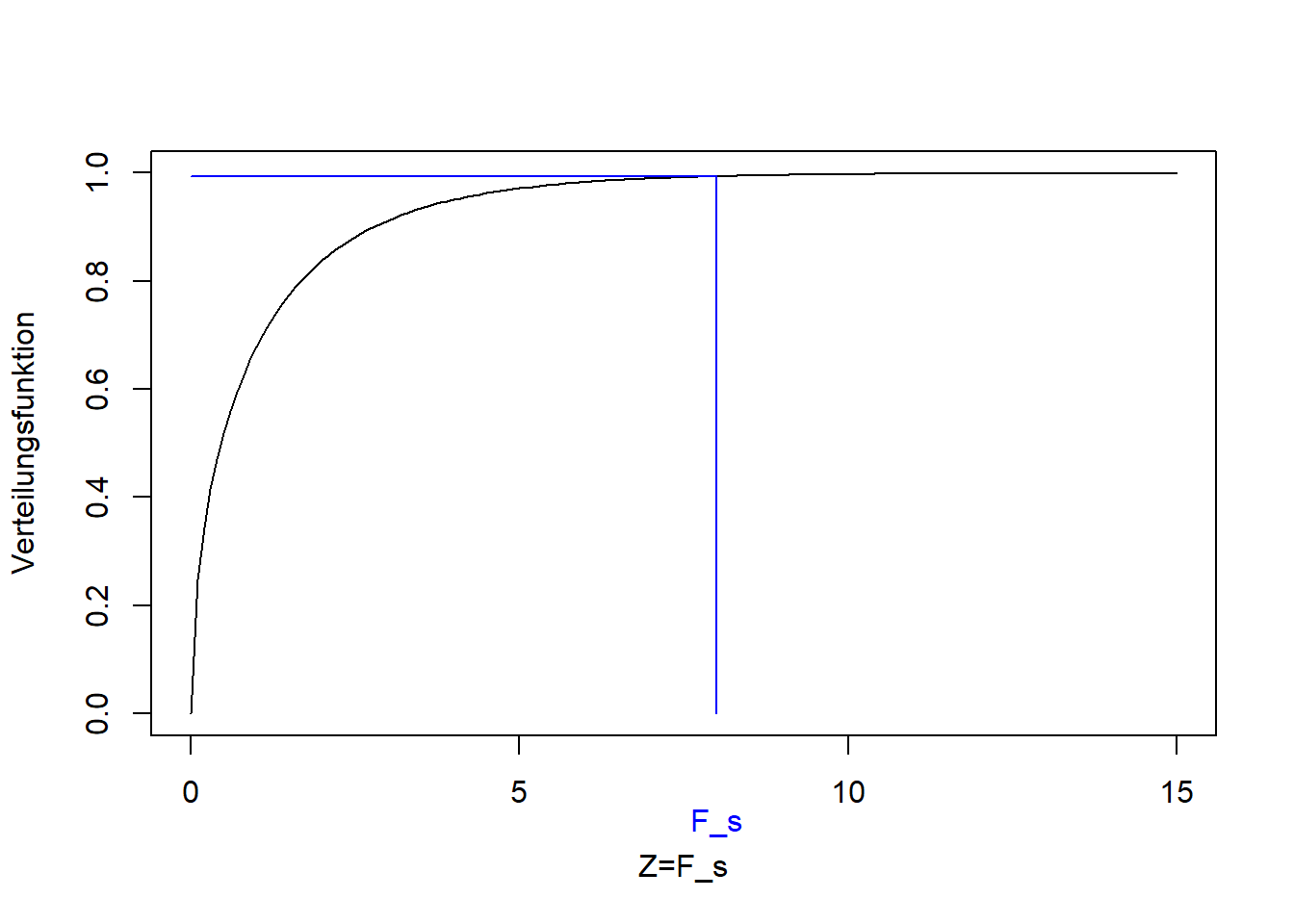
Abbildung 10.4: Verteilungsfunktion der F-Verteilung der F-Statistik \(F_s\). Blau: Bestimmter Wert für \(F_s\) und entsprechender Wert der Verteilungsfunktion.
Für die Regression der Reisedaten ist der p-Wert wesentlich kleiner als das konventionelle Signifikanzniveau \(\alpha=0.01\), daher lehnen wir die Nullhypothese ab und bezeichnen die Regression als “statistisch signifikant” in der klassischen Interpretation. Schauen wir uns die ANOVA-Tabelle für das Beispiel an:
## Analysis of Variance Table
##
## Response: zeit_morgens
## Df Sum Sq Mean Sq F value Pr(>F)
## distanz 1 14149 14149 91.9 1e-13 ***
## Residuals 60 9242 154
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Im Vergleich zu Tabelle 10.3 lässt R die letzte Zeile (\(SSY\)) weg und tauscht die Spalten “Quadratsumme” und “Freiheitsgrad”.
Der Anteil der Varianz (in \(y\)-Richtung), der durch das Modell erklärt wird, wird außerdem mit dem Bestimmtheitsmaß (\(r^2\)) ausgedrückt: \[\begin{equation} r^2=\frac{SSY-SSE}{SSY}=1-\frac{SSE}{SSY} \tag{10.14} \end{equation}\] Das Bestimmtheitsmaß ist der Korrelationskoeffizient nach Bravais-Pearson zum Quadrat (vgl. Kapitel 5).
Wie wir an Gleichung (10.14) sehen, wenn das Modell nicht mehr Variation als die Gesamtvariation um den Mittelwert erklärt, d.h. \(SSE=SSY\) ist, dann ist \(r^2=0\). Umgekehrt, wenn das Modell perfekt zu den Daten passt, d.h. \(SSE=0\) ist, dann ist \(r^2=1\). Werte dazwischen stellen unterschiedliche Grade der Anpassungsgüte dar. Das kann wiederum mit Abbildung 10.3 veranschaulicht werden, wobei der linke Teil \(SSY\) und der rechte Teil \(SSE\) verdeutlicht.
Wenn es darum geht, Modelle unterschiedlicher Komplexität (d.h. mit mehr oder weniger Parametern) mit \(r^2\) zu vergleichen, dann ist es sinnvoll, das Bestimmtheitsmaß mit der Anzahl der Modellparameter zu korrigieren, da komplexere Modelle (mehr Parameter) automatisch zu besseren Anpassungen führen, einfach aufgrund der größeren Flexibilität, die komplexere Modelle bei der Anpassung an die Daten haben. Dies führt zum korrigierten \(r^2\): \[\begin{equation} \bar r^2=1-\frac{\frac{SSE}{df_{SSE}}}{\frac{SSY}{df_{SSY}}}=1-\frac{SSE}{SSY} \cdot \frac{df_{SSY}}{df_{SSE}} \tag{10.15} \end{equation}\]
Rechnen wir \(r^2\) und \(\bar r^2\) für die Regression der Reisedaten aus:
## [1] 0.6049## [1] 0.5983D.h. es werden rund 60% der Varianz in den Reisezeit-Daten durch das lineare Modell mit Entfernung als Prädiktor erklärt.
10.6 Konfidenzintervalle der Parameterschätzer
Da die Modellanpassung nicht perfekt ist, haben die Parameterschätzer Standardfehler, d.h. sie werden wie andere statistische Kennzahlen als Realisationen eines Zufallsprozesses interpretiert. Das führt uns zu Konfidenzintervallen und t-Tests auf Signifikanz der einzelnen Parameter.
Der Standardfehlern für \(\hat\beta_0\) ist: \[\begin{equation} s_{\hat\beta_0}=\sqrt{\frac{\sum_{i=1}^{n}x_i^2}{n} \cdot \frac{s^2}{SSX}} \tag{10.16} \end{equation}\]
Wenn wir diese Formel in ihre einzelnen Teile zerlegen, sehen wir: Je mehr Datenpunkte \(n\) wir haben, desto kleiner ist der Standardfehler, d.h. desto mehr Vertrauen haben wir in die Schätzung. Außerdem gilt, je größer die Variation in \(x\) (\(SSX\)), desto kleiner der Standardfehler. Beide Effekte machen intuitiv Sinn: Je mehr Datenpunkte wir haben und je mehr Ausprägungen von \(x\) wir abgedeckt haben, desto sicherer können wir sein, dass unsere Stichprobe aussagekräftig für die Grundgesamtheit ist. Umgekehrt gilt: Je größer die Fehlervarianz \(s^2\), d.h. je kleiner die Erklärungskraft unseres Modells, desto größer der Standardfehler. Und je mehr \(x\)-Datenpunkte von Null entfernt sind, d.h. je größer \(\sum_{i=1}^{n}x_i^2\), desto geringer ist unser Vertrauen in den Achsenabschnitt (wo \(x=0\) ist) und damit steigt der Standardfehler für \(\hat\beta_0\).
Der Standardfehler für \(\hat\beta_1\) ist: \[\begin{equation} s_{\hat\beta_1}=\sqrt{\frac{s^2}{SSX}} \tag{10.17} \end{equation}\] Hier gilt die gleiche Interpretation wie zuvor, außer dass es keinen Einfluss der Größe der \(x\)-Datenpunkte gibt.
Wir können auch einen Standardfehler für neue Vorhersagen \(\hat y\) für gegebene \(\hat x\) festlegen: \[\begin{equation} s_{\hat y}=\sqrt{s^2 \cdot \left(\frac{1}{n}+\frac{\left(\hat x-\bar x\right)^2}{SSX}\right)} \tag{10.18} \end{equation}\]
Dieselbe Interpretation gilt auch hier, nur dass jetzt ein zusätzlicher Term \(\left(\hat x-\bar x\right)^2\) auftaucht, der besagt, je weiter der neue \(x\)-Wert vom Zentrum der ursprünglichen Daten (den Trainings- oder Kalibrierungsdaten) entfernt ist, desto größer ist der Standardfehler der neuen Vorhersage, d.h. desto geringer ist die Zuversicht, dass sie korrekt ist.
Anmerkung: Die Formeln für die Standardfehler ergeben sich aus den grundlegenden Annahmen der linearen Regression, auf die wir weiter unten eingehen werden. Die mathematische Herleitung lassen wir hier aus.
Aus den Standardfehlern können wir Konfidenzintervalle für die Parameterschätzer wie folgt berechnen (vgl. Konfidenzintervall des Mittelwertschätzers (Kapitel 8)): \[\begin{equation} \Pr\left(\hat\beta_0-t_{n-2;0.975} \cdot s_{\hat\beta_0}\leq \beta_0\leq \hat\beta_0+t_{n-2;0.975} \cdot s_{\hat\beta_0}\right)=0.95 \tag{10.19} \end{equation}\]
Gleichung (10.19) ist das zentrale 95%-Konfidenzintervall, in dem der wahre Parameterwert, hier \(\beta_0\), mit einer Wahrscheinlichkeit von 0.95 liegt.26
Wir können das Intervall auch wie folgt schreiben: \[\begin{equation} KI=\left[\hat\beta_0-t_{n-2;0.975} \cdot s_{\hat\beta_0};\hat\beta_0+t_{n-2;0.975} \cdot s_{\hat\beta_0}\right] \tag{10.20} \end{equation}\]
Wie bei dem Konfidenzintervall des Mittelwertschätzers (Kapitel 8) liegt das Konfidenzintervall symmetrisch um den Parameterschätzer \(\hat\beta_0\) und ergibt sich aus einer t-Verteilung mit dem Parameter \(n-2\) (Freiheitsgrade), deren Breite durch den Standardfehler \(s_{\hat\beta_0}\) moduliert wird. Erinnern Sie sich, dass die Breite der t-Verteilung ebenfalls durch den Stichprobenumfang kontrolliert wird und mit zunehmendem \(n\) immer schmaler wird.
Die gleichen Formeln gelten für \(\beta_1\) und \(y\): \[\begin{equation} \Pr\left(\hat\beta_1-t_{n-2;0.975} \cdot s_{\hat\beta_1}\leq \beta_1\leq \hat\beta_1+t_{n-2;0.975} \cdot s_{\hat\beta_1}\right)=0.95 \tag{10.21} \end{equation}\] \[\begin{equation} \Pr\left(\hat y-t_{n-2;0.975} \cdot s_{\hat y}\leq y\leq \hat y+t_{n-2;0.975} \cdot s_{\hat y}\right)=0.95 \tag{10.22} \end{equation}\]
Die Formeln für die Konfidenzintervalle (Gleichungen (10.19), (10.21) und (10.22)) ergeben sich aus den Grundannahmen der linearen Regression (vgl. Kapitel 8): Die Residuen sind unabhängig identisch verteilt (u.i.v.) gemäß einer Normalverteilung, d.h. \(\epsilon_i\sim N(0,\sigma)\), und das lineare Modell ist korrekt. Dann lässt sich mathematisch zeigen, dass \(\frac{\hat\beta_0-\beta_0}{s_{\hat\beta_0}}\), \(\frac{\hat\beta_1-\beta_1}{s_{\hat\beta_1}}\) und \(\frac{\hat y-y}{s_{\hat y}}\) \(t_{n-2}\)-verteilt sind (t-Verteilung mit \(n-2\) Freiheitsgraden). Da das zentrale 95%-Konfidenzintervall einer \(t_{n-2}\)-verteilten Zufallsvariablen \(Z\) \(\Pr\left(-t_{n-2;0.975}\leq Z\leq t_{n-2;0. 975}\right)=0.95\) ist (Abbildung 8.2), können wir jeden der oben genannten drei Terme für \(Z\) einsetzen und die Ungleichung umstellen, um zu den Gleichungen (10.19), (10.21) und (10.22) zu gelangen (vgl. Kapitel 8).
Die Unsicherheit der Parameterschätzer wird mit Hilfe eines t-Tests ermittelt (vgl. Kapitel 9.2). Die Nullhypothese ist, dass die wahren Parameterwerte (bezogen auf die Grundgesamtheit) gleich Null sind: \[\begin{equation} H_0:\beta_0=0 \tag{10.23} \end{equation}\] \[\begin{equation} H_0:\beta_1=0 \tag{10.24} \end{equation}\]
Diese Hypothese wird gegen die Alternativhypothese getestet, dass die wahren Parameterwerte ungleich Null sind: \[\begin{equation} H_1:\beta_0\neq 0 \tag{10.25} \end{equation}\] \[\begin{equation} H_1:\beta_1\neq 0 \tag{10.26} \end{equation}\]
Die Teststatistiken sind: \[\begin{equation} t_s=\frac{\hat\beta_0-0}{s_{\hat\beta_0}}\sim t_{n-2} \tag{10.27} \end{equation}\] \[\begin{equation} t_s=\frac{\hat\beta_1-0}{s_{\hat\beta_1}}\sim t_{n-2} \tag{10.28} \end{equation}\]
Die t-Verteilungen der Teststatistiken ergeben sich wiederum aus den oben erwähnten Regressionsannahmen. Die Annahmen sind die gleichen wie beim üblichen t-Test der Mittelwerte (Kapitel 9.2), außer dass im Fall der linearen Regression die Residuen als u.i.v. normal angenommen werden, während im Fall der Mittelwerte die tatsächlichen Datenpunkte \(y\) als u.i.v. normal angenommen werden.
Analog zum üblichen 2-seitigen t-Test ist der p-Wert definiert als: \[\begin{equation} 2 \cdot \Pr\left(t>|t_s|\right)=2 \cdot \left(1-F_t\left(|t_s|\right)\right) \tag{10.29} \end{equation}\]
Mit einem konventionellen Signifikanzniveau von \(\alpha=0.01\) gelangen wir zu einem kritischen Wert der Teststatistik \(t_c=t_{n-2;0.995}\), bei dessen Überschreitung, bzw. Unterschreitung von \(-t_c\), wir die Nullhypothese ablehnen und die Parameterschätzer in der klassischen Interpretation als “signifikant” bezeichnen.
Jetzt verstehen wir auch die restlichen Informationen des Outputs der lm() Funktion (s. oben):
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 21.53 3.4700 6.205 5.568e-08
## distanz 2.19 0.2285 9.584 1.040e-13Wie bereits oben erwähnt steht die Zeile “(Intercept)” für \(\beta_0\) und die Zeile “distanz” (in diesem Fall) für \(\beta_1\). In der Spalte “Estimate” stehen die Werte der Parameterschätzer. In der Spalte “Std. Error” stehen deren Standardfehler (Gleichungen (10.16) und (10.17)). In der Spalte “t value” stehen die entsprechenden Werte der Teststatistik (Gleichungen (10.27) und (10.28)). In der Spalte “Pr(>|t|)” stehen die p-Werte der t-Tests (Gleichung (10.29)). Wir sehen, dass in unserem Beispiel beide Parameter in der klassischen Interpretation “signifikant” sind (die p-Werte sind wesentlich kleiner als das konventionelle \(\alpha=0.01\)).
Mit der Information der Konfidenzintervalle der Parameterschätzer und der Vorhersagen können wir jetzt die Regressionsgerade mit Konfidenzintervall darstellen. Nur dann ist die Darstellung vollständig. Es gibt zwei Arten von Konfidenzintervallen: das Konfidenzintervall der Regressionsgeraden, in das die Konfidenzintervalle der beiden Parameterschätzer (Gleichungen (10.19) und (10.21)) eingehen, und das Konfidenzintervall tatsächlicher Werte der abhängigen Variable \(y\) für Werte der unabhängigen Variable \(x\), d.h. das Konfidenzintervalle der Vorhersagen (Gleichung (10.22)).
Das erste Konfidenzintervall beschreibt damit die Unsicherheit des Trends durch die Punktwolke, der meistens von primärem Interesse ist:
Das zweite Konfidenzintervall beschreibt die Unsicherheit der Vorhersage neuer einzelner Werte von \(y\), die natürlich wesentlich größer ist:
10.7 Annahmen der Regression
Da die o.g. Schätzer und wahrscheinlichkeitstheoretischen Aussagen nur unter bestimmten Modellannahmen gültig sind, müssen wir diese Annahmen bei jeder Regression testen. Folgende Annahmen ergeben sich aus der Maximum-Likelihood-Theorie (vgl. Schätzen von Verteilungsparametern, Kapitel 8):
- Die Residuen sind unabhängig, in diesem Fall gibt es keine serielle Korrelation in der Residuengrafik (s. unten) - dies kann mit dem Durbin-Watson-Test getestet werden
- Die Residuen sind normalverteilt - dies kann visuell mit Hilfe des Quantil-Quantil-Diagramms (QQ-Plot) und dem Residuen-Histogramm beurteilt werden, und kann mit dem Kolmogorov-Smirnov-Test (Kapitel 9.6) und dem Shapiro-Wilk-Test getestet werden
- Die Varianz ist für alle Residuen konstant (die Residuen sind homoskedastisch), d.h. es erfolgt kein “Auffächern” der Residuen
Sind diese Annahmen nicht erfüllt, können wir auf Datentransformation, gewichtete Regression oder Generalisierte Lineare Modelle zurückgreifen. Letzteres wird z.B. im Master Global Change Geography unterrichtet.
Eine erste nützliche diagnostische Darstellung ist die der Residuen in Serie, d.h. nach Index \(i\), um zu sehen, ob es ein Muster aufgrund des Datenerfassungsprozesses gibt. Für unser Beispiel:
Die Residuen zeigen kein erkennbares Muster, das gegen die Unabhängigkeit der Residuen sprechen würde.
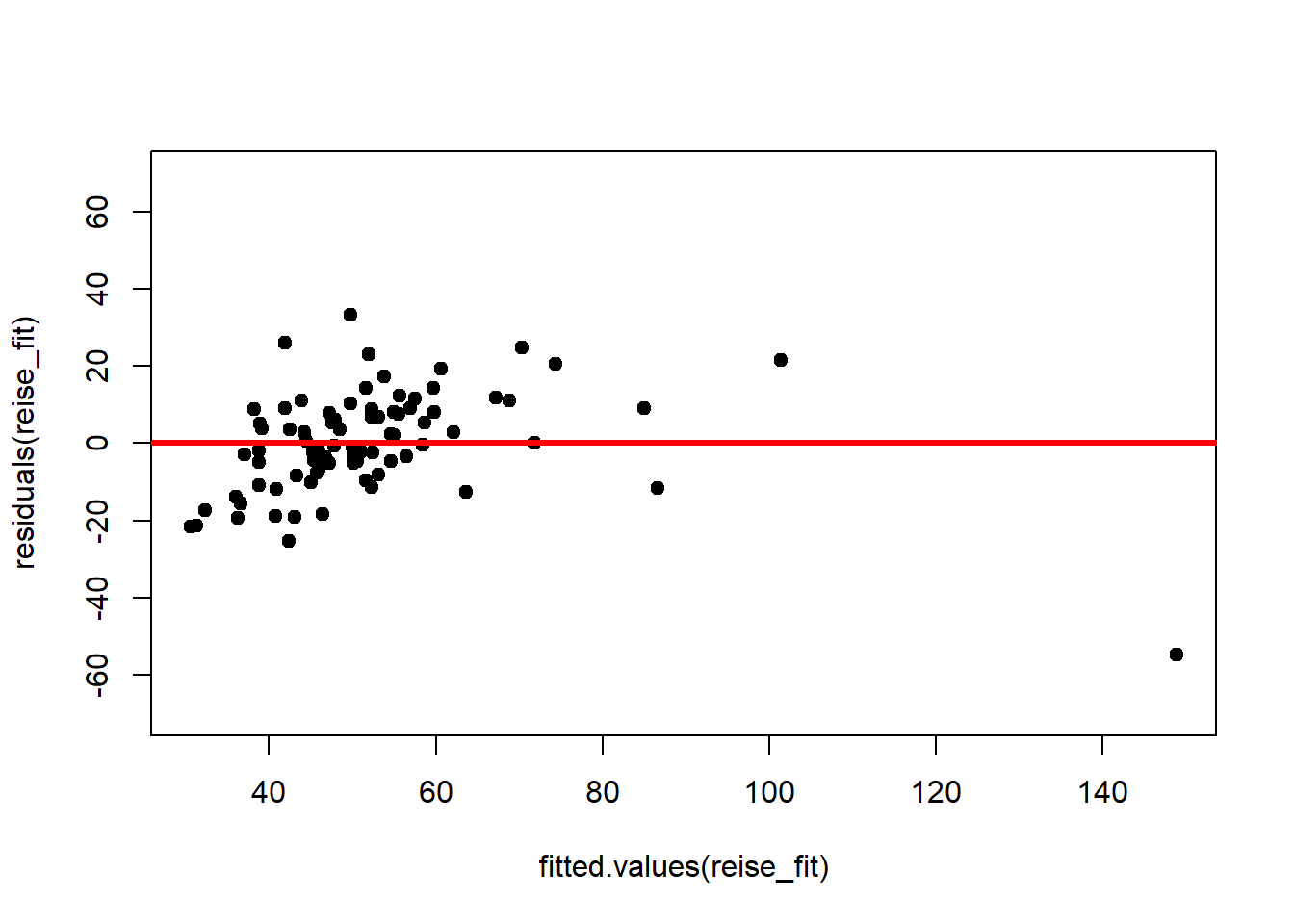
Wir sollten auch die Residuen nach dem modellierten Wert von \(y\) plotten, um zu sehen, ob es ein Muster als Funktion der Größenordnung von \(y\) gibt:
Auch hier sieht man kein erkennbares Muster.
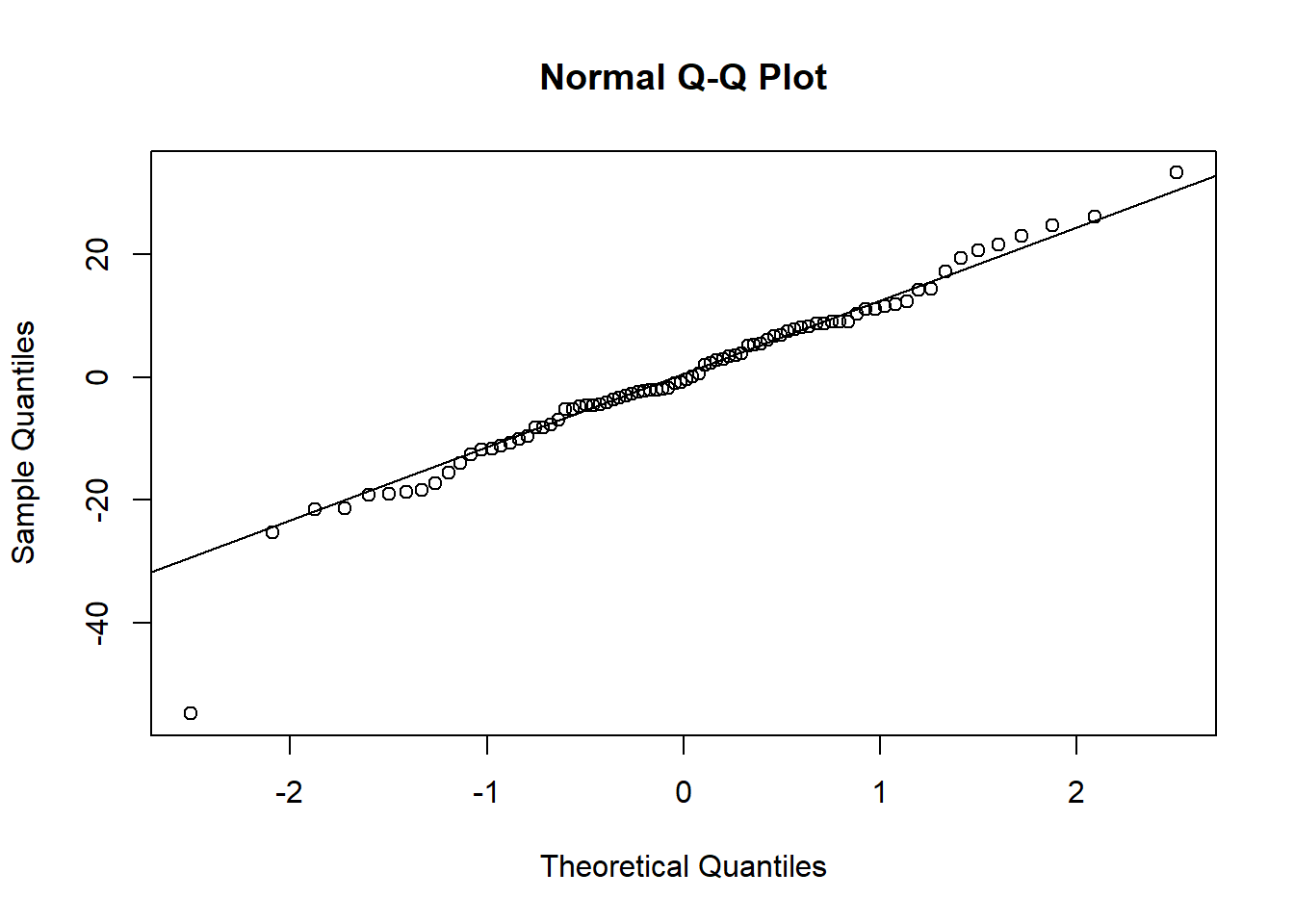
Die Annahme, dass die Residuen normalverteilt sind, kann anhand des QQ-Plots beurteilt werden (vgl. Kapitel 8.4):
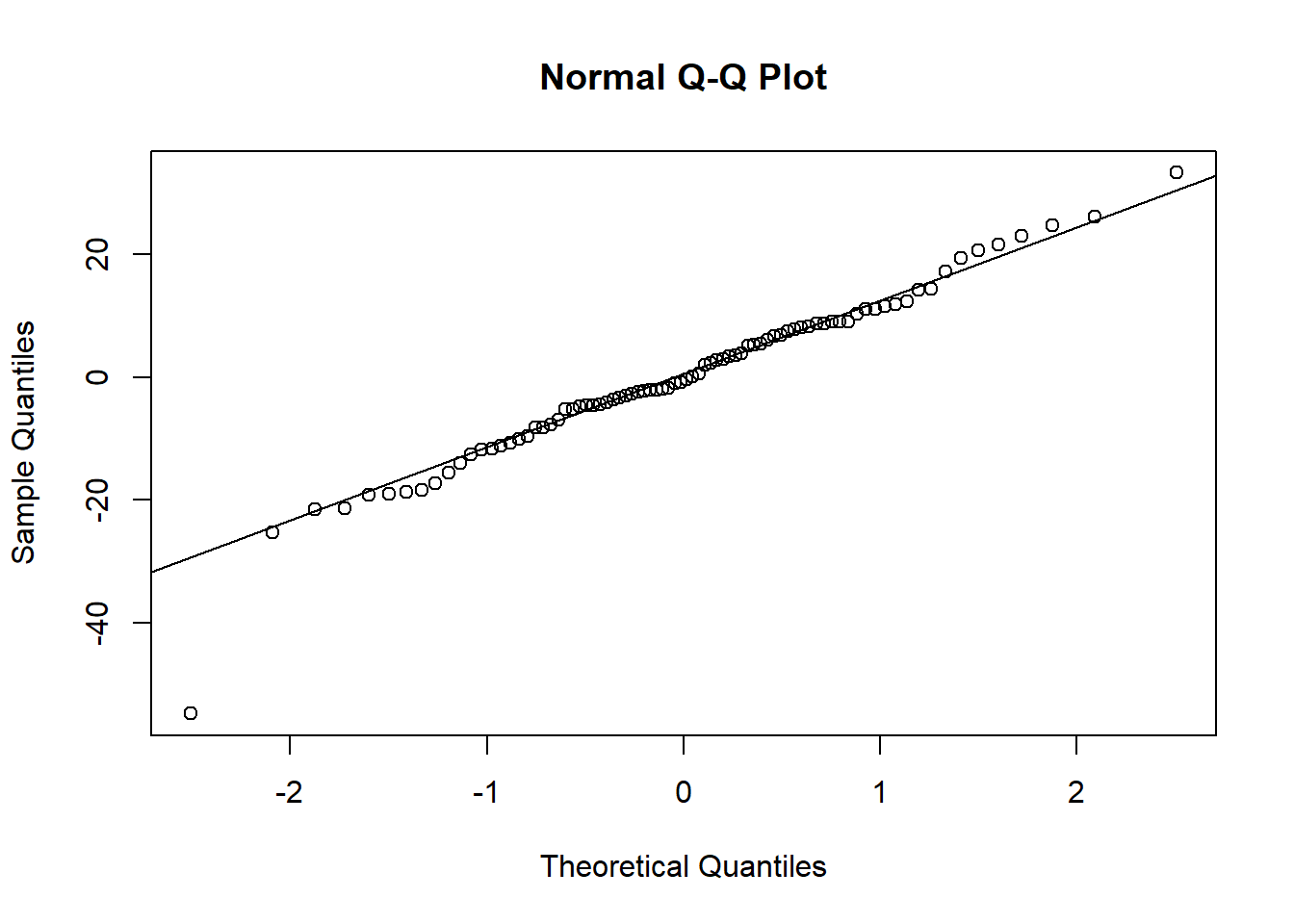
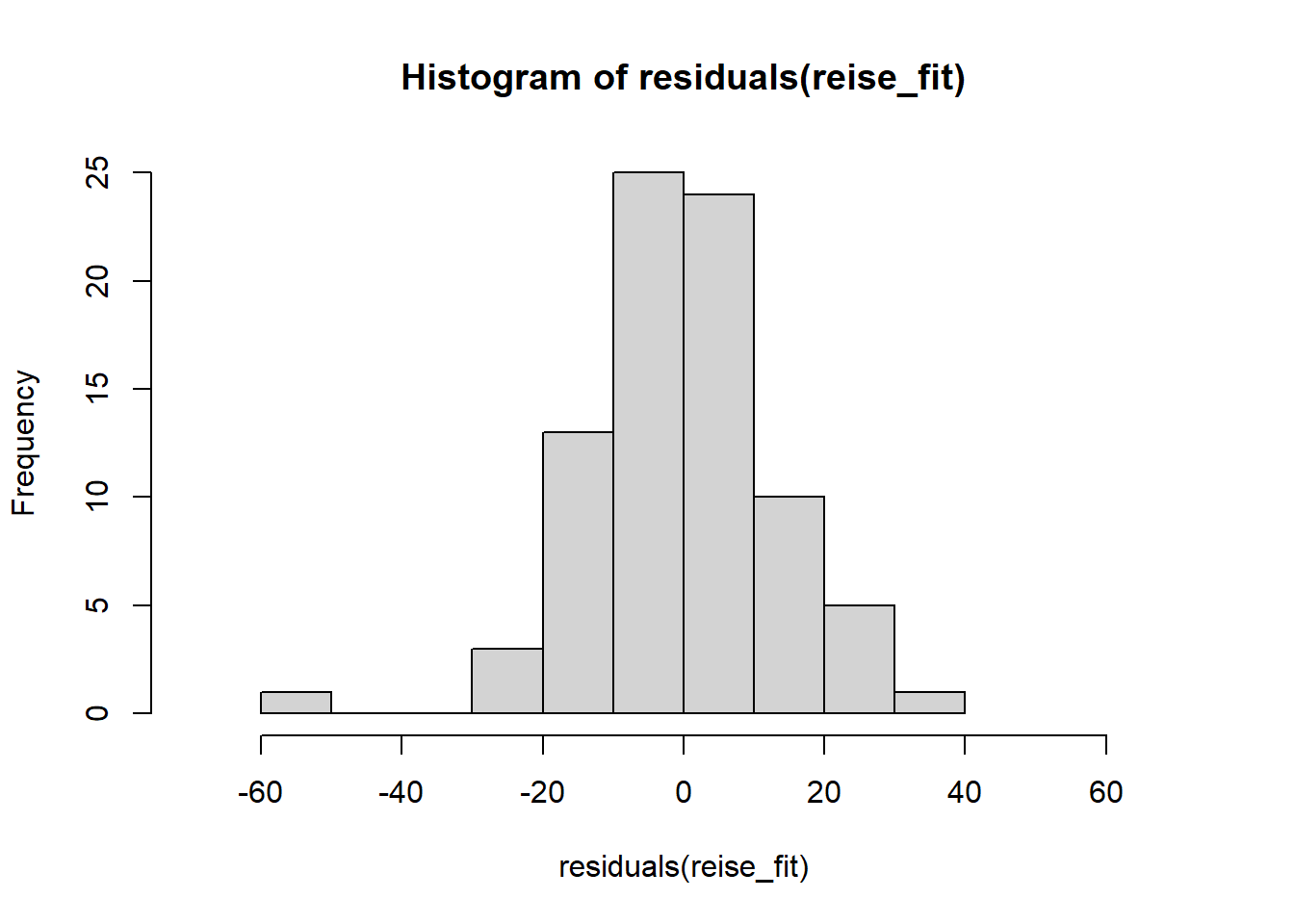
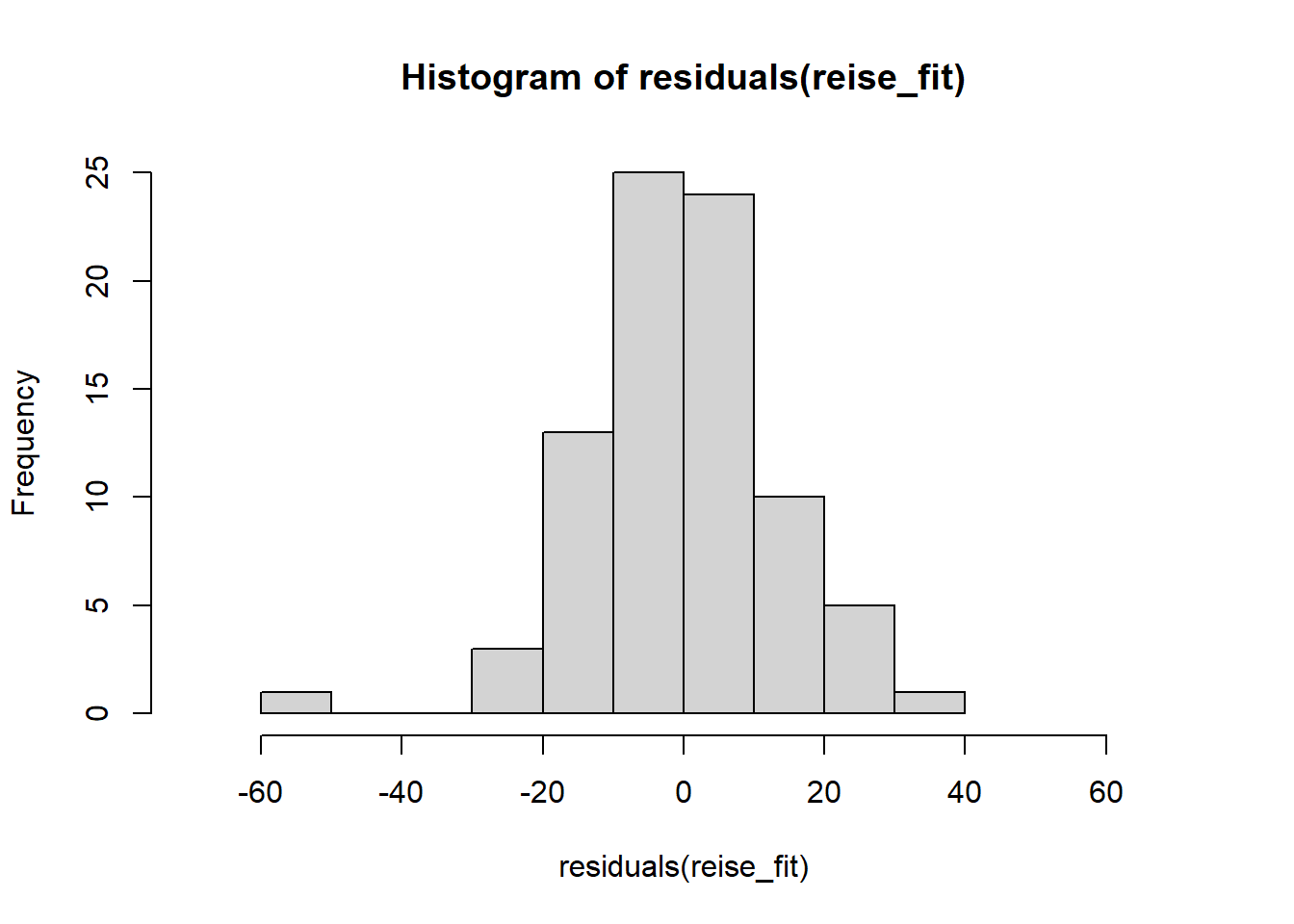
Die Annahme normalverteilter Residuen erscheint plausibel, auch wenn die Verteilung etwas spitzer als eine Normalverteilung erscheint und leicht rechtsschief. Vgl. https://xiongge.shinyapps.io/QQplots/. Das kann man auch am Histogramm der Residuen sehen, einer weiteren nützlichen Darstellung:
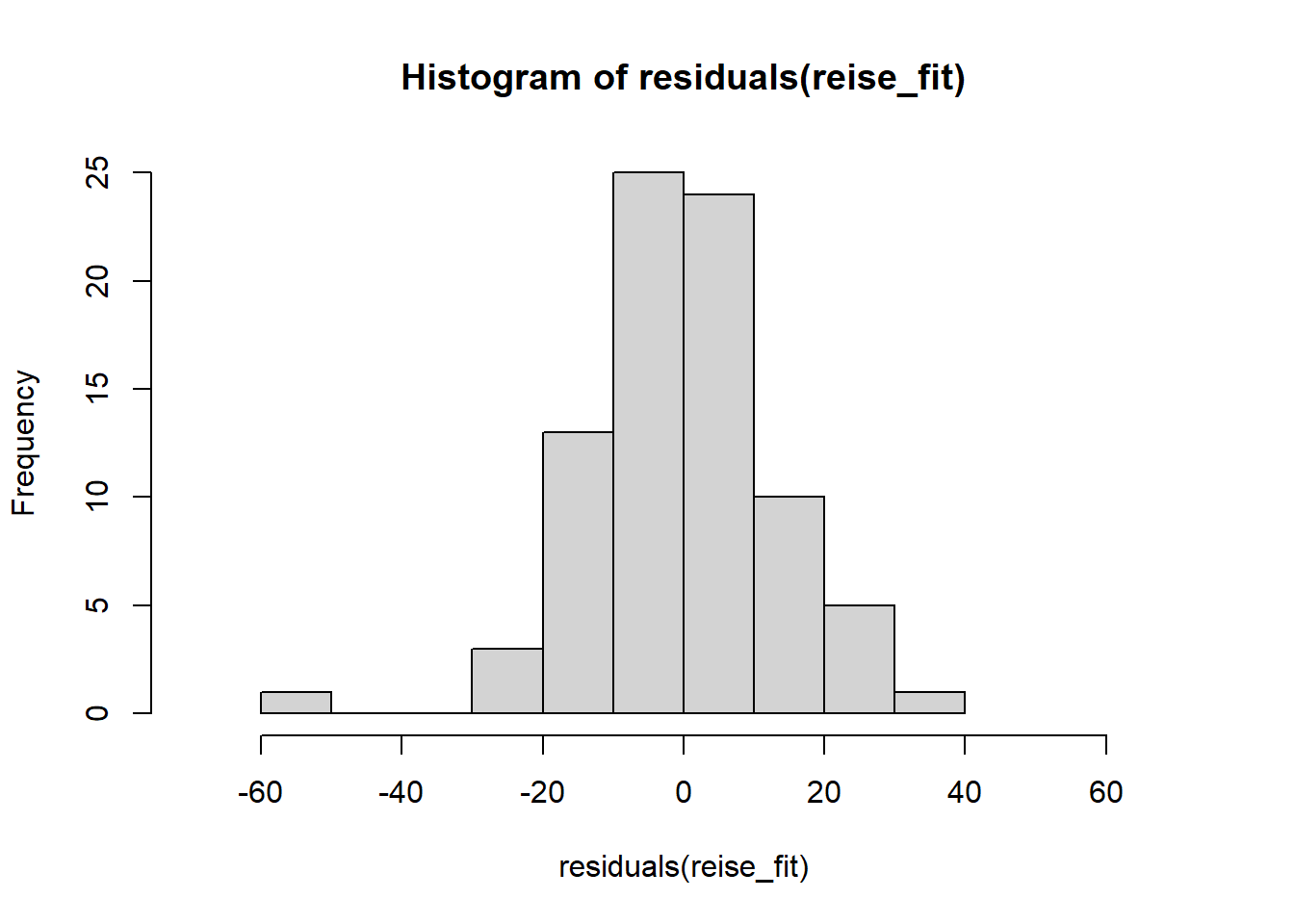
Auch ein formaler KS-Test gibt keinen Anlass, die Normalverteilungsannahme der Residuen abzulehnen:
## Warning in ks.test.default(res, "pnorm", 0, sd(res)):
## ties should not be present for the one-sample
## Kolmogorov-Smirnov test##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: res
## D = 0.13, p-value = 0.2
## alternative hypothesis: two-sidedWir können also die Regressionsannahmen in unserem Fall als hinreichend erfüllt betrachten und mit den ermittelten Parameterschätzern und deren Unsicherheiten weiterarbeiten.
10.8 ANOVA als Regressionsproblem
Abschließend sei noch die ANOVA im engen Sinn als Regressionsproblem vorgestellt, auch um die in Kapitel 9.5 angesprochenen Probleme der Vergleiche zwischen Kategorien zu umgehen. Da die ANOVA als Generalisierung des t-Test verstanden werden kann (auf mehr als 2 Kategorien), ist die Regression gleichzeitig eine Generalisierung des t-Tests.
Kehren wir dazu zu dem Ertragsbeispiel aus Crawley (2012) zurück (Abbildung 9.4): Hat Bodenart einen Einfluss auf Ertrag?
Anders als in Kapitel 9.5 analysieren wir jetzt aber die Daten mit der lm() Funktion, wobei die ANOVA Tabelle wie gesagt im Hintergrund aufgestellt wird:
ertrag_long <- ertrag %>%
pivot_longer(everything()) %>%
mutate(name = factor(name))
# lineare Regression von Ertrag mit Bodenart als Prädiktor
ertrag_fit <- lm(value ~ name, data = ertrag_long)
summary(ertrag_fit)##
## Call:
## lm(formula = value ~ name, data = ertrag_long)
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.5 -1.8 0.3 1.7 7.1
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 14.30 1.08 13.23 2.6e-13 ***
## nameSand -4.40 1.53 -2.88 0.0077 **
## nameTon -2.80 1.53 -1.83 0.0781 .
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.42 on 27 degrees of freedom
## Multiple R-squared: 0.239, Adjusted R-squared: 0.183
## F-statistic: 4.24 on 2 and 27 DF, p-value: 0.025Wir haben also eine lineare Regression durchgeführt mit Ertrag als abhängige Variable und Bodenart als kategorische (!) unabhängige Variable (Prädiktor). R interpretiert das wie folgt (siehe Ausgabe): Der Achsenabschnitt “(Intercept)” ist jetzt der mittlere Ertrag für eine der 3 Bodenart-Kategorien (in diesem Fall “Lehm”, da das Wort alphabetisch zuerst kommt). Dies ist die sogenannte Basiskategorie. Der mittlere Ertrag auf Lehm ist also 14.3 wie bereits in Kapitel 9.5 errechnet. Die beiden weiteren Zeilen “nameSand” und “nameTon” sind jetzt die Ertragsunterschiede von “Sand” bzw. “Ton” im Vergleich zur Basiskategorie “Lehm”. Sand liefert also im Mittel 4.4 weniger Ertrag als Lehm und Ton im Mittel 2.8 weniger Ertrag als Lehm. Auch diese Zahlenwerte kennen wir schon aus Kapitel 9.5. Die lm() Funktion hat also aus den 3 Kategorien einen Achsenabschnitt und 2 “Steigungen” gemacht, wenn man so will.
Der Vorteil ist jetzt, dass wir Ertragsunterschiede zwischen Kategorien und deren Unsicherheiten direkt aus den Ergebnissen der lm() Funktion ablesen können, zumindest im Vergleich zur Basiskategorie. Wir sehen dadurch, dass Sand tatsächlich “signifikant” weniger Ertrag liefert als Lehm (p-Wert kleiner als 0.01), Ton aber nicht. Es steckt also mehr Information in dieser Analyse als in der ANOVA im engen Sinn. Gleichzeitig passen wir nur ein Modell an und umgehen das Problem vieler einzelner t-Tests. Nur für den Vergleich von Sand und Ton müssten wir die Ergebnisse nochmal umrechnen, was an dieser Stelle aber zu weit führt. Als Ausblick können Sie das gerne in Crawley (2012) nachlesen. Eine Residuenanalyse würde analog zur Regression im engen Sinn erfolgen (Kapitel 10.7).
Literatur
Auch Regressionsprobleme mit nominal oder ordinal skalierten abhängigen Variablen sind mathematisch ähnlich. Das wird z.B. im Masterstudiengang Global Change Geography gelehrt.↩︎
Summenregel: wenn \(y=u(t) \pm v(t)\) dann \(\frac{dy}{dt}=\frac{du}{dt} \pm \frac{dv}{dt}\)↩︎
Kettenregel: wenn \(y=f[g(t)]\) dann \(\frac{dy}{dt}=\frac{df[g]}{dg} \cdot \frac{dg}{dt}\), d.h. “äußere mal innere Ableitung”↩︎
Wenn wir jedoch die unabhängige Variable “distanz” zentrieren würden, d.h. von allen Datenpunkten den Mittelwert abziehen würden, dann ergäbe sich ein Achsenabschnitt, der die Reisezeit für die mittlere Entfernung darstellen würde.↩︎
Wahrscheinlichkeit heißt hier wieder, dass bei wiederholtem Stichprobenziehen in 95% der Fälle das so konstruierte Konfidenzintervall den wahren Wert \(\beta_0\) umschließt und in 5% der Fälle nicht.↩︎